题目内容
某市教育主管部门为了弘扬民族文化,在全市各中学开展汉字听写大赛,某学校经过七轮选拔,最后选出甲乙两名选手代表本校参加市里比赛,甲乙两名选手七轮比赛得分情况如下表所示:
(1)根据表中的数据分析,哪位选手成绩更为稳定?
(2)从甲选手的7次成绩中随机抽取两次成绩,求抽出的两次成绩的分数差值至少是3分的概率.
| 甲 | 86 | 94 | 89 | 88 | 91 | 90 | 92 |
| 乙 | 88 | 89 | 90 | 91 | 93 | 92 | 87 |
(2)从甲选手的7次成绩中随机抽取两次成绩,求抽出的两次成绩的分数差值至少是3分的概率.
考点:古典概型及其概率计算公式,极差、方差与标准差
专题:概率与统计
分析:(1)首先要求甲乙的方差,再根据方差越小波动越小,成绩越稳定,得出答案,
(2)一一列举出从甲选手的七次成绩中随机抽取2次的所有基本事件,抽取的两次分数差距至少(3分)基本的事件,根据古典概型的概率的求法,问题得以解决.
(2)一一列举出从甲选手的七次成绩中随机抽取2次的所有基本事件,抽取的两次分数差距至少(3分)基本的事件,根据古典概型的概率的求法,问题得以解决.
解答:
解:(Ⅰ)由题意得
=
=90,
=
=90,
S甲2=
[(86-96)2+(94-90)2+(89-90)2+(88-90)2+(91-90)2+(90-90)2+(92-90)2]=6,
S乙2=
[(88-90)2+(89-90)2+(90-90)2+(91-90)2+(93-90)2+(92-90)2+(87-90)2]=4,
因为6>4,所以乙选手成绩更稳定.
(Ⅱ)从甲选手的七次成绩中随机抽取2次的所有基本事件为:(86,94),(86,89),(86,88),(86,91),(86,90),(86,92),(94,89),(94,88),(94,91),
(94,90),(94,92),(89,88),(89,91),(89,90),(89,92),(88,91),(88,90),(88,92),(91,90),(91,92),(90,92)共21种情况,
则抽取的两次分数差距至少(3分)的事件包含:(86,94),(86,89),(86,91),(86,90),(86,92),(94,89),(94,88),(94,91),(94,90),(89,92),(88,91),(88,92)共12种情况.
则抽取的两次成绩差距至少3分的概率P=
=
.
. |
| x甲 |
| 86+94+89+88+91+90+92 |
| 7 |
. |
| x乙 |
| 88+89+90+91+93+92+87 |
| 7 |
S甲2=
| 1 |
| 7 |
S乙2=
| 1 |
| 7 |
因为6>4,所以乙选手成绩更稳定.
(Ⅱ)从甲选手的七次成绩中随机抽取2次的所有基本事件为:(86,94),(86,89),(86,88),(86,91),(86,90),(86,92),(94,89),(94,88),(94,91),
(94,90),(94,92),(89,88),(89,91),(89,90),(89,92),(88,91),(88,90),(88,92),(91,90),(91,92),(90,92)共21种情况,
则抽取的两次分数差距至少(3分)的事件包含:(86,94),(86,89),(86,91),(86,90),(86,92),(94,89),(94,88),(94,91),(94,90),(89,92),(88,91),(88,92)共12种情况.
则抽取的两次成绩差距至少3分的概率P=
| 12 |
| 21 |
| 4 |
| 7 |
点评:本题主要考查了方差的求法,以及古典概型的概率的求法,求方差是注意计算的准确程度,求概率时要一一列举满足条件的基本事件.

练习册系列答案
相关题目
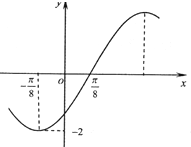 已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<