Question

已知⊙O₁和⊙O₂相交于A，B两点，过A点作⊙O₁的切线交⊙O₂于点E，连接EB并延长交⊙O₁于点C，直线CA交⊙O₂于点D．
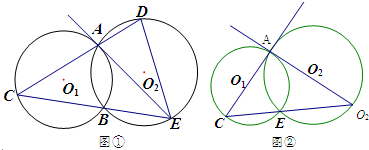
（Ⅰ）当点D与点A不重合时（如图①），证明ED²=EB•EC；
（Ⅱ）当点D与点A重合时（如图②），若BC=2，BE=6，求⊙O₂的直径长．

Answer 1

考点：与圆有关的比例线段

专题：选作题,立体几何

分析：（Ⅰ）连接AB，在EA的延长线上取点F，证明∠ABC=∠DAE，∠DAE=∠ADE，可得EA=ED，利用EA²=EB•EC，即可证明结论；
（Ⅱ）证明AC与AE分别为⊙O₁和⊙O₂的直径，由切割线定理知：EA²=BE•CE，即可得出结论．

解答： （Ⅰ）证明：连接AB，在EA的延长线上取点F．
∵AE是⊙O₁的切线，切点为A，
∴∠FAC=∠ABC，．…（1分）
∵∠FAC=∠DAE，
∴∠ABC=∠DAE，
∵∠ABC是⊙O₂内接四边形ABED的外角，
∴∠ABC=∠ADE，…（2分）
∴∠DAE=∠ADE．…（3分）
∴EA=ED，
∵EA²=EB•EC，
∴ED²=EB•EC．…（5分）
（Ⅱ）解：当点D与点A重合时，直线CA与⊙O₂只有一个公共点，
∴直线CA与⊙O₂相切．…（6分）
如图②所示，由弦切角定理知：∠PAC=∠ABC，∠MAE=∠ABE，
∵∠PAC=∠MAE，
∴∠ABC=∠ABE=90°
∴AC与AE分别为⊙O₁和⊙O₂的直径．…（8分）
∴由切割线定理知：EA²=BE•CE，而CB=2，BE=6，CE=8
∴EA²=6×8=48，AE=4

3

．
故⊙O₂的直径为4

3

．…（10分）

点评：本题考查与圆有关的比例线段，考查切割线定理、弦切角定理，考查学生分析解决问题的能力，属于中档题．