题目内容
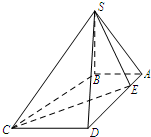如图，在四棱锥S-ABCD中，SB⊥底面ABCD．底面ABCD为梯形，AB⊥AD，AB∥CD，AB=1，AD=3，CD=2．若点E是线段AD上的动点，则满足∠SEC=90°的点E的个数是考点：空间中直线与平面之间的位置关系,直线与平面垂直的性质
专题：计算题,空间位置关系与距离
分析：连接BE，则问题转化为在梯形ABCD中，点E是线段AD上的动点，求满足BE⊥CE的点E的个数．
解答：
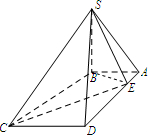解：连接BE，则
∵SB⊥底面ABCD，∠SEC=90°，
∴BE⊥CE．
故问题转化为在梯形ABCD中，点E是线段AD上的动点，求满足BE⊥CE的点E的个数．
设AE=x，则DE=3-x，
∵AB⊥AD，AB∥CD，AB=1，AD=3，CD=2，
∴10=1+x2+4+（3-x）2，
∴x2-3x+2=0，
∴x=1或2，
∴满足BE⊥CE的点E的个数为2，
∴满足∠SEC=90°的点E的个数是2．
故答案为：2．
解：连接BE，则∵SB⊥底面ABCD，∠SEC=90°，
∴BE⊥CE．
故问题转化为在梯形ABCD中，点E是线段AD上的动点，求满足BE⊥CE的点E的个数．
设AE=x，则DE=3-x，
∵AB⊥AD，AB∥CD，AB=1，AD=3，CD=2，
∴10=1+x2+4+（3-x）2，
∴x2-3x+2=0，
∴x=1或2，
∴满足BE⊥CE的点E的个数为2，
∴满足∠SEC=90°的点E的个数是2．
故答案为：2．
点评：本题考查空间中直线与平面之间的位置关系，考查学生的计算能力，问题转化为在梯形ABCD中，点E是线段AD上的动点，求满足BE⊥CE的点E的个数是关键．
练习册系列答案
相关题目
若aij表示n×n阶矩阵，如图所示中第i行、第j列的元素（i、j=1，2，3，…，n），其中若aij=321，则i+j=三次函数y=ax3-x在（-∞，+∞）内是减函数，则（ ）
| A、a≤0 | ||
| B、a=1 | ||
| C、a=2 | ||
D、a=
|
己知双曲线
-
=1（a＞0，b＞0）离心率为2，有一个焦点与抛物线y2=4x的焦点重合，则ab的值为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|