题目内容

已知0＜x＜1，则x2（1-x）的最大值是
 
．
考点：基本不等式
专题：不等式的解法及应用
分析：变形利用均值不等式即可得出．
解答： 解：∵0＜x＜1，∴x2（1-x）=
1
2
x•x(2-2x)≤
1
2
(
x+x+2-2x
3
)3=
4
27
，当且仅当x=
2
3
时取等号．
∴x2（1-x）的最大值是
4
27
．
故答案为：
4
27
．
点评：本题考查了均值不等式，属于基础题．
练习册系列答案
相关题目
已知sinα=-
5
5
，tanβ=-
1
3
，且α、β∈（-
π
2
，0）．
（1）求tan2β的值
（2）求tan（α+β）的值．
定义在R上的函数f（x），其图象是连续不断的，如果存在非零常数λ（λ∈R），使得对任意的x∈R，都有f（x+λ）=λf（x），则称f（x）为“倍增函数”，λ为“倍增系数”．下列命题正确的是
 
（写出所有正确命题的编号）．
①函数f（x）=x是倍增函数，且倍增系数λ=1；
②函数f（x）=e-x是倍增函数，且倍增系数λ∈（0，1）；
③若函数f（x）是可导倍增函数，则其导函数f′（x）也是倍增函数；
④若函数f（x）是倍增系数λ=-1的倍增函数，则f（x）也是周期函数；
⑤若函数f（x）=cos2ωx（ω＞0）是倍增函数，则ω=
kπ
2
（k∈N*）．
如图：已知四面体A-BCD的外接球的球心O在线段BD上，且AO⊥平面BCD，BC=
3
2
BD，若四面体A-BCD的体积为
3
2
，则球O的表面积为
 
．
函数y=x2（-
1
2
≤x≤
1
2
）图象上一点P，以点P为切点的切线为直线l，则直线l的倾斜角的范围是
 
．
已知函数f（x）及其导数f′（x），若存在x0，使得f（x0）=f′（x0），则称x0是f（x）的一个“巧值点”，下列函数中，有“巧值点”的函数个数是
 
（只填数字）
①f（x）=x2
②f（x）=e-x
③f（x）=lnx
④f（x）=x+
1
x
．
已知f（x）=（x-2）2，x∈（-1，3），函数f（x+1）的单调减区间为
 
．
设集合A={x|0≤x＜1}，B={x|1≤x≤3}，函数f（x）=
3x，x∈A
6-2x，x∈B
，当x0∈A且f[f（x0）]∈A时，x0的取值范围是
 
．
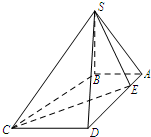如图，在四棱锥S-ABCD中，SB⊥底面ABCD．底面ABCD为梯形，AB⊥AD，AB∥CD，AB=1，AD=3，CD=2．若点E是线段AD上的动点，则满足∠SEC=90°的点E的个数是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网