题目内容
三次函数y=ax3-x在(-∞,+∞)内是减函数,则( )
| A、a≤0 | ||
| B、a=1 | ||
| C、a=2 | ||
D、a=
|
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:由y′=3ax2-1≤0,得a≤
,而
>0,从而a≤0.
| 1 |
| 3x2 |
| 1 |
| 3x2 |
解答:
解:∵三次函数y=ax3-x在(-∞,+∞)内是减函数,
∴y′=3ax2-1≤0,
∴a≤
,而
>0,
∴a≤0,
故选:A.
∴y′=3ax2-1≤0,
∴a≤
| 1 |
| 3x2 |
| 1 |
| 3x2 |
∴a≤0,
故选:A.
点评:本题考察了函数的单调性,导数的应用,是一道基础题.

练习册系列答案
相关题目
已知点P是椭圆
+
=1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且F1M⊥MP,则|
|的取值范围是( )
| x2 |
| 16 |
| y2 |
| 8 |
| OM |
| A、(0,3) | ||
B、(2
| ||
| C、(0,4) | ||
D、(0,2
|
设函数f(x)=xa+1(a∈Q)的定义域为[-b,-a]∪(a,b],其中0<a<b,且f(x)在[a,b]上的最大值为6,最小值为3,则f(x)在[-b,-a]上的最大值与最小值的和是( )
| A、-5 | B、9 |
| C、-5或9 | D、以上不对 |
函数y=|x+1|+2的最小值是( )
| A、0 | B、-1 | C、2 | D、3 |
已知函数y=f(x)的导函数y=f′(x)的图象如图,则( )
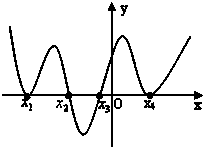

| A、函数f(x)有2个极大值点,2个极小值点 |
| B、函数f(x)有1个极大值点,1个极小值点 |
| C、函数f(x)有3个极大值点,1个极小值点 |
| D、函数f(x)有1个极大值点,3个极小值点. |
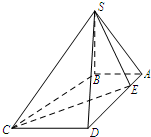 如图,在四棱锥S-ABCD中,SB⊥底面ABCD.底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是
如图,在四棱锥S-ABCD中,SB⊥底面ABCD.底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是