题目内容
 若aij表示n×n阶矩阵,如图所示中第i行、第j列的元素(i、j=1,2,3,…,n),其中若aij=321,则i+j=
若aij表示n×n阶矩阵,如图所示中第i行、第j列的元素(i、j=1,2,3,…,n),其中若aij=321,则i+j=考点:归纳推理,高阶矩阵
专题:推理和证明
分析:改变数字的形式,找到相应的规律,得ai1=1+2+…+n=
,从求出i,j的值.
| n(n+1) |
| 2 |
解答:
解:把矩阵的数字改为如下形式,第i行第一个数字不变,最后一个数字代表第j列的元素的第一个数字,
13,2
6,5,4
10,9,8,7
15,14,13,12,11
21,20,19,18,17,16
…
可以看出每行的数字都是连续递减的,第一列的数为1,3,6,…,
∴ai1=1+2+…+n=
,
∵
=325>321,
∴325是第25行的第一个数字,则321是第25行的第5个数,
∴对于矩阵而言,321则位于第(25-5+1)行,第5列,
即i=21,j=5,
故i+j=21+5=26.
故答案为:26.
13,2
6,5,4
10,9,8,7
15,14,13,12,11
21,20,19,18,17,16
…
可以看出每行的数字都是连续递减的,第一列的数为1,3,6,…,
∴ai1=1+2+…+n=
| n(n+1) |
| 2 |
∵
| 25×(25+1) |
| 2 |
∴325是第25行的第一个数字,则321是第25行的第5个数,
∴对于矩阵而言,321则位于第(25-5+1)行,第5列,
即i=21,j=5,
故i+j=21+5=26.
故答案为:26.
点评:本题考查数列的通项,考查矩阵变换的性质,突出累加法求通项的考查,属于中档题.

练习册系列答案
相关题目
已知和式S=
,当n趋向于∞时,S无限趋向于一个常数A,则A可用定积分表示为( )
| 12+22+32+…+n2 |
| n3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知点P是椭圆
+
=1(xy≠0)上的动点,F1、F2为椭圆的左、右焦点,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且F1M⊥MP,则|
|的取值范围是( )
| x2 |
| 16 |
| y2 |
| 8 |
| OM |
| A、(0,3) | ||
B、(2
| ||
| C、(0,4) | ||
D、(0,2
|
不等式a2+4≥4a中等号成立的条件是( )
| A、a=±2 | B、a=2 |
| C、a=-2 | D、a=4 |
已知数列{an}满足an+1=an-an-1(n≥2)a1=1,a2=3,记Sn=a1+a2+…+an,则下列结论正确的是( )
| A、a2014=-1,S2014=2 |
| B、a2014=-3,S2014=5 |
| C、a2014=-3,S2014=2 |
| D、a2014=-1,S2014=5 |
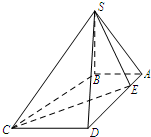 如图,在四棱锥S-ABCD中,SB⊥底面ABCD.底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是
如图,在四棱锥S-ABCD中,SB⊥底面ABCD.底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是