题目内容
已知定义在R上的周期函数y=f(x)的图象如图所示,则f(10π)= .

考点:函数的值
专题:函数的性质及应用
分析:图象知函数周期为2,所以f(10π)=f(10π-30),由此能求出结果.
解答:
解:由图象知函数周期为2
∴f(10π)=f(10π-30)
=2-(10π-30)
=32-10π.
故答案为:32-10π.
∴f(10π)=f(10π-30)
=2-(10π-30)
=32-10π.
故答案为:32-10π.
点评:本题考查函数值的求法,解题时要认真审题,注意函数的周期性的合理运用.

练习册系列答案
相关题目
设函数f(x)=xa+1(a∈Q)的定义域为[-b,-a]∪(a,b],其中0<a<b,且f(x)在[a,b]上的最大值为6,最小值为3,则f(x)在[-b,-a]上的最大值与最小值的和是( )
| A、-5 | B、9 |
| C、-5或9 | D、以上不对 |
已知直线a和平面α,则能推出a∥α的是( )
| A、存在一条直线b,a∥b,且b∥α |
| B、存在一条直线b,a⊥b,且b⊥α |
| C、存在一个平面β,a?β,且α∥β |
| D、存在一个平面β,a∥β,且α∥β |
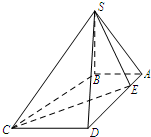 如图,在四棱锥S-ABCD中,SB⊥底面ABCD.底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是
如图,在四棱锥S-ABCD中,SB⊥底面ABCD.底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是