题目内容
14.若过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)右顶点A且与其中一条渐近线平行,又与另一条渐近线交于点B,满足三角形AOB的面积为$\frac{{a}^{2}}{4}$,则该双曲线的离心率e为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
分析 求得A(a,0)求出双曲线的渐近线方程,设出直线AB的方程为y=$\frac{b}{a}$(x-a),代入y=-$\frac{b}{a}$x,解方程可得B的坐标,再由△AOB的面积为$\frac{1}{2}$•|OA|•|yB|,化简,结合离心率公式即可得到所求值.
解答 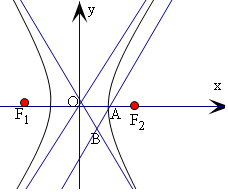 解:过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)右顶点A为(a,0),
解:过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)右顶点A为(a,0),
与其中一条渐近线y=$\frac{b}{a}$x平行,
又与另一条渐近线y=-$\frac{b}{a}$x交于点B,
可得直线AB的方程为y=$\frac{b}{a}$(x-a),
代入y=-$\frac{b}{a}$x可得x=$\frac{a}{2}$,y=-$\frac{1}{2}$b,即有B($\frac{a}{2}$,-$\frac{1}{2}$b),
则△AOB的面积为$\frac{1}{2}$•|OA|•|yB|=$\frac{1}{2}$a•$\frac{1}{2}$b=$\frac{{a}^{2}}{4}$,
化为a=b,则c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{2}$a,
即有e=$\frac{c}{a}$=$\sqrt{2}$.
故选:A.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的渐近线方程,以及联立直线方程求交点,考查三角形的面积公式的应用,以及运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.设函数f(x)=$\left\{\begin{array}{l}{1+lo{g}_{2}(2-x),x<1}\\{2x-1,x≥1}\end{array}\right.$,则f(-2)+f(2)=( )
| A. | 3 | B. | 6 | C. | 5 | D. | 12 |
9.下列函数中,定义域与y=lnx相同的函数是( )
| A. | y=x | B. | y=$\sqrt{x}$ | C. | y=$\frac{1}{x}$ | D. | y=$\frac{1}{\sqrt{x}}$ |
19.若函数f(x)=$\frac{{x}^{2}+a}{x+1}$在x=l处取得极值,则a=( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
20. 某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验.甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在[60,100]区间内(满分100分),并绘制频率分布直方图如图,两个班人数均为60人,成绩80分及以上为优良.
某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验.甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在[60,100]区间内(满分100分),并绘制频率分布直方图如图,两个班人数均为60人,成绩80分及以上为优良.
(1)根据以上信息填好下列2×2联表,并判断出有多大的把握认为学生成绩优良与班级有关?
(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选2人来作书面发言,求2人都来自甲班的概率.
下面的临界值表供参考:
(以下临界值及公式仅供参考${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,n=a+b+c+d)
 某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验.甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在[60,100]区间内(满分100分),并绘制频率分布直方图如图,两个班人数均为60人,成绩80分及以上为优良.
某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验.甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在[60,100]区间内(满分100分),并绘制频率分布直方图如图,两个班人数均为60人,成绩80分及以上为优良.(1)根据以上信息填好下列2×2联表,并判断出有多大的把握认为学生成绩优良与班级有关?
| 是否优良 班级 | 优良(人数) | 非优良(人数) | 合计 |
| 甲 | |||
| 乙 | |||
| 合计 |
下面的临界值表供参考:
| P(x2?k) | 0.10 | 0.05 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
1.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的命题是( )
| A. | m⊥α,n?β,m⊥n⇒α⊥β | B. | α⊥β,α∩β=m,n⊥m⇒n⊥β | ||
| C. | α⊥β,m⊥α,n∥β⇒m⊥n | D. | α∥β,m⊥α,n∥β⇒m⊥n |
 如图,已知正方体ABCD-A1B1C1D1的棱长为1.
如图,已知正方体ABCD-A1B1C1D1的棱长为1.