题目内容
已知f（x）是定义在R上的奇函数，且当x＞0时，f（x）=（
）x，求函数f（x）的解析式．
| 1 |
| 2 |
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：首先，当x=0时，f（0）=0，然后，设x＜0，则-x＞0，然后，借助于函数为奇函数，进行求解即可．
解答：
解：因为f（x）是定义在R上的奇函数，
所以，当x=0时，f（0）=0，
设x＜0，则-x＞0，
∴f(-x)=(
)-x=（（2-1）-x=2x，
∵f（-x）=-f（x），
∴-f（x）=2x，
∴f（x）=-2x，
∴f(x)=
．
所以，当x=0时，f（0）=0，
设x＜0，则-x＞0，
∴f(-x)=(
| 1 |
| 2 |
∵f（-x）=-f（x），
∴-f（x）=2x，
∴f（x）=-2x，
∴f(x)=
|
点评：本题重点考查了函数的奇偶性与函数的解析式相结合知识点，涉及到指数的运算性质，属于中档题，难度中等．
练习册系列答案
相关题目
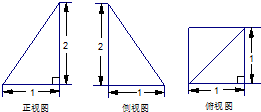
已知一几何体三视图如图，则其体积为（ ）
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
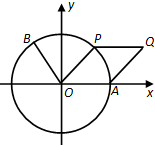如图，点A是单位圆与x轴正半轴的交点，点B（-