Question

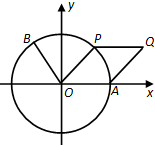如图，点A是单位圆与x轴正半轴的交点，点B（-

3

5

，

4

5

），∠AOB=α，

π

2

＜α＜π，|

OP

|=1，∠AOP=θ，0＜θ＜

π

2

．
（1）若cos（α-θ）=-

16

65

，求点P的坐标；
（2）若四边形OAQP为平行四边形且面积为S，求S+

OA

•

OQ

的最大值．

Answer 1

考点：两角和与差的余弦函数,数量积的坐标表达式

专题：三角函数的求值

分析：（1）设点P的坐标为（m，n），由题意可得cosα=-

3

5

，sinα=

4

5

．由cos（α-θ）=-

16

65

，可得sin（α-θ）=

63

65

，求得m=cosθ=cos[α-（α-θ）]、以及sinθ=sin[α-（α-θ）]=sinαcos（α-θ）-cosαsin（α-θ）的值，从而可得点P的坐标．
（2）利用数量积的定义，结合三角函数的图象和性质，计算即可．

解答： 解：（1）设点P的坐标为（m，n），由点B(-

3

5

，

4

5

)，∠AOB=α，可知cosα=-

3

5

，sinα=

4

5

．
又|

OP

|=1，∠AOP=θ，0＜θ＜

π

2

，∴m=cosθ，n=sinθ．
∵cos（α-θ）=-

16

65

，∴sin（α-θ）=

63

65

，
于是由可得m=cosθ=cos[α-（α-θ）]=cosαcos（α-θ）+sinαsin（α-θ）=-

3

5

×（-

16

65

）+

4

5

×

63

65

=

12

13

，
sinθ=sin[α-（α-θ）]=sinαcos（α-θ）-cosαsin（α-θ）=

4

5

×(-

16

65

)-(-

3

5

)×

63

65

=

5

13

，
因|

OP

|=1，故点的坐标为（

12

13

，

5

13

）． 
（2）由已知可得A（1，0），P（cosθ，sinθ），

OP

=(cosθ，sinθ)，
因为平行四边形，故

OQ

=

OA

+

OP

=(1+cosθ，sinθ)，
∵S=sinθ，∴S+

OA

•

OQ

=sinθ+1+cosθ=

2

sin（θ+

π

4

）+1，
∵0＜θ＜

π

2

，故

2

sin（θ+

π

4

）+1 的最大值为

2

+1，
即S+

OA

•

OQ

的最大值为

2

+1．

点评：本题主要考查平面向量数量积的应用以及两角和差的正切公式，以及向量和三角函数的综合问题，考查学生的运算能力，属于中档题．