题目内容

1．为了普及环保知识，增强环保意识，某大学从大学理工类专业的A班和文史专业的B班各抽取20名同学参加环保知识测试，统计得到成绩与专业的列联表：
优秀非优秀总计
A班14620
B班71320
总计211940
附：参考公式及数据：
①K2统计量：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$（其中n=a+b+c+d）；
②独立性检验的临界值表：
P（K≥k0）0.0500.010
k03.8416.635
（　　）
A．有99%的把握认为环保知识测试成绩与专业有关
B．有99%的把握认为环保知识测试成绩与专业无关
C．有95%的把握认为环保知识测试成绩与专业无关
D．有95%的把握认为环保知识测试成绩与专业有关

分析 根据表中数据计算统计量K2，参考临界数据得出结论．

解答 解：根据表中数据，计算统计量
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$=$\frac{40{×（14×13-7×6）}^{2}}{20×20×21×19}$≈4.912＞3.841，
参考临界数据知，有95%的把握认为环保知识测试成绩与专业有关．
故选：D．

点评 本题考查了独立性检验的应用问题，是基础题．

练习册系列答案
相关题目
17．给出下列等式：$\sqrt{2}=2cos\frac{π}{4}$，$\sqrt{2+\sqrt{2}}=2cos\frac{π}{8}$，$\sqrt{2+\sqrt{2+\sqrt{2}}}=2cos\frac{π}{16}$，…请从中归纳出第n（n∈N*）个等式：$\underbrace{\sqrt{2+\sqrt{2+…+\sqrt{2}}}}_{n个根号}$=$2cos\frac{π}{{{2^{n+1}}}}$．
18．某四棱台的三视图如图所示，则该四棱台的体积是（　　）
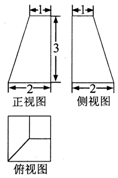
A．7B．6C．5D．4
9．在平面直角坐标系式xOy中，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1（-c，0）、F2（c，0），已知（1，e）和（e，$\frac{\sqrt{3}}{2}$）都在椭圆上，其中e为椭圆的离心率．
（1）求椭圆C的方程；
（2）过点F2的直线l与椭圆C相交于P，Q两点，且$\overrightarrow{P{F}_{2}}$•$\overrightarrow{{F}_{1}Q}$+$\overrightarrow{{F}_{1}{F}_{2}}$•$\overrightarrow{Q{F}_{2}}$=4，求直线l的方程．
16．在△ABC中，a，b，c分别为A、B、C的对边，且满足2（a2-b2）=2accosB+bc
（1）求A
（2）D为边BC上一点，CD=3BD，∠DAC=90°，求tanB．
6．下列命题中，正确的是（　　）
A．若a＞b，c＞d，则ac＞bdB．若ac＞bc，则a＞b
C．若a＞b，c＞d，则a-c＞b-dD．若$\frac{a}{{c}^{2}}$＜$\frac{b}{{c}^{2}}$，则a＜b
13．在△ABC中，内角A，B，C所对的边分别为a，b，c，b（1-2cosA）=2acosB．
（1）若b=2，求c的值；
（2）若a=1，tanA=2$\sqrt{2}$，求△ABC的面积．
10．研究性学习小组要从6名（其中男生4人，女生2人）成员中任意选派3人去参加某次社会调查．
（Ⅰ）在男生甲被选中的情况下，求女生乙也被选中的概率；
（Ⅱ）设所选3人中女生人数为ξ，求ξ的分布列及数学期望．
11．下列函数中，周期为π，且以直线x=$\frac{π}{3}$为对称轴的是（　　）
A．$y=sin（\frac{x}{2}+\frac{π}{3}）$B．$y=sin（2x-\frac{π}{6}）$C．$y=cos（2x-\frac{π}{6}）$D．$y=tan（x+\frac{π}{6}）$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网