题目内容
13.在△ABC中,内角A,B,C所对的边分别为a,b,c,b(1-2cosA)=2acosB.(1)若b=2,求c的值;
(2)若a=1,tanA=2$\sqrt{2}$,求△ABC的面积.
分析 (1)由正弦定理得sinB(1-2cosA)=2sinAcosB,
即sinB=2(sinAcosB+cosAsinB)=2sinC,得b=2c.
(2)由tanA=$\frac{sinA}{cosA}$,=2$\sqrt{2}$,解得cosA=$\frac{1}{3}$,sinA=$\frac{2\sqrt{2}}{3}$
由(1)b=2c,由余弦定理有cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{4{c}^{2}+{c}^{2}-1}{2bc}=\frac{1}{3}$,解c2=$\frac{3}{11}$,即可求面积.
解答 解:(1)∵b(1-2cosA)=2acosB,
∴由正弦定理得sinB(1-2cosA)=2sinAcosB,
即sinB=2(sinAcosB+cosAsinB)=2sinC
所以b=2c,∵b=2,∴c=1;…(5分)
(2)∵tanA=$\frac{sinA}{cosA}$=2$\sqrt{2}$,∴sinA=2$\sqrt{2}cosA$
∵sin2A+cos2A=1,
解得cosA=$\frac{1}{3}$,∴sinA=$\frac{2\sqrt{2}}{3}$
由(1)b=2c
由余弦定理有cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{4{c}^{2}+{c}^{2}-1}{2bc}=\frac{1}{3}$,解得c2=$\frac{3}{11}$
∴s△ABC=$\frac{1}{2}bcsinA={c}^{2}sinA=\frac{3}{11}•\frac{2\sqrt{2}}{3}=\frac{2\sqrt{2}}{11}$.
点评 本题考查了正余弦定理的应用,考查了计算能力,属于中档题.

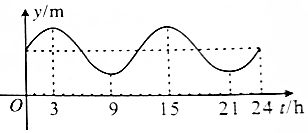
| A. | 6h | B. | 8h | C. | 12h | D. | 24h |
| 优秀 | 非优秀 | 总计 | |
| A班 | 14 | 6 | 20 |
| B班 | 7 | 13 | 20 |
| 总计 | 21 | 19 | 40 |
①K2统计量:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d);
②独立性检验的临界值表:
| P(K≥k0) | 0.050 | 0.010 |
| k0 | 3.841 | 6.635 |
| A. | 有99%的把握认为环保知识测试成绩与专业有关 | |
| B. | 有99%的把握认为环保知识测试成绩与专业无关 | |
| C. | 有95%的把握认为环保知识测试成绩与专业无关 | |
| D. | 有95%的把握认为环保知识测试成绩与专业有关 |
| A. | $\frac{9}{4}$ | B. | 2 | C. | 3 | D. | 4 |
 如图,已知正四棱柱(底面为正方形,侧棱与底面垂直)ABCD-A1B1C1D1的底面边长为3,侧棱长为4,连结A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱(底面为正方形,侧棱与底面垂直)ABCD-A1B1C1D1的底面边长为3,侧棱长为4,连结A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.