题目内容
16.在△ABC中,a,b,c分别为A、B、C的对边,且满足2(a2-b2)=2accosB+bc(1)求A
(2)D为边BC上一点,CD=3BD,∠DAC=90°,求tanB.
分析 (1)将2(a2-b2)=2accosB+bc化解结合余弦定理可得答案.
(2)因为∠DAC=$\frac{π}{2}$,所以AD=CD•sinC,∠DAB=$\frac{π}{6}$.利用正弦定理即可求解.
解答 解:(1)由题意2accosB=a2+c2-b2,
∴2(a2-b2)=a2+c2-b2+bc.
整理得a2=b2+c2+bc,
由余弦定理:a2=b2+c2-2bccosA
可得:bc=-2bccosA
∴cosA=-$\frac{1}{2}$,
∵0<A<π
∴A=$\frac{2π}{3}$.
(Ⅱ)∵∠DAC=$\frac{π}{2}$,
∴AD=CD•sinC,∠DAB=$\frac{π}{6}$.
在△ABD中,有$\frac{AD}{sinB}=\frac{BD}{sin∠DAB}$,
又∵CD=3BD,
∴3sinC=2sinB,
由C=$\frac{π}{3}$-B,得$\frac{{3\sqrt{3}}}{2}$cosB-$\frac{3}{2}$sinB=2sinB,
整理得:tanB=$\frac{{3\sqrt{3}}}{7}$.
点评 本题考查了正弦、余弦定理的灵活运用和计算能力.属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
12.设集合A={x|(x+4)(x-4)>0},B={x|-2<x≤6},则A∩B等于( )
| A. | (-2,4) | B. | (4,-2) | C. | (-4,6) | D. | (4,6] |
13.已知集合A={x|y=log2(x-1)},集合B={x|(x+1)(x-2)≤0},则A∪B=( )
| A. | [-1,+∞) | B. | (1,2] | C. | (1,+∞) | D. | [-1,2] |
4.如图,某港口一天的水深变化曲线近似满足函数y=Asin$\frac{π}{6}$t+k,则水深从最小值变化到最大值至少需要( )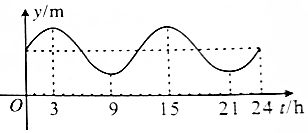

| A. | 6h | B. | 8h | C. | 12h | D. | 24h |
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,P为双曲线右支上一点(异于右顶点),△PF1F2的内切圆与x轴切于点(2,0),过F2作直线l与双曲线交于A,B两点,若使|AB|=b2的直线l恰有三条,则双曲线离心率的取值范围是( )
| A. | (1,$\sqrt{2}$) | B. | (1,2) | C. | ($\sqrt{2}$,+∞) | D. | (2,+∞) |
1.为了普及环保知识,增强环保意识,某大学从大学理工类专业的A班和文史专业的B班各抽取20名同学参加环保知识测试,统计得到成绩与专业的列联表:
附:参考公式及数据:
①K2统计量:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d);
②独立性检验的临界值表:
( )
| 优秀 | 非优秀 | 总计 | |
| A班 | 14 | 6 | 20 |
| B班 | 7 | 13 | 20 |
| 总计 | 21 | 19 | 40 |
①K2统计量:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d);
②独立性检验的临界值表:
| P(K≥k0) | 0.050 | 0.010 |
| k0 | 3.841 | 6.635 |
| A. | 有99%的把握认为环保知识测试成绩与专业有关 | |
| B. | 有99%的把握认为环保知识测试成绩与专业无关 | |
| C. | 有95%的把握认为环保知识测试成绩与专业无关 | |
| D. | 有95%的把握认为环保知识测试成绩与专业有关 |
5.已知△ABC三个内角A、B、C所对的边分别为a、b、c,且3sinA=a,sinB=$\frac{3}{4}$,则b等于( )
| A. | $\frac{9}{4}$ | B. | 2 | C. | 3 | D. | 4 |