题目内容
17.给出下列等式:$\sqrt{2}=2cos\frac{π}{4}$,$\sqrt{2+\sqrt{2}}=2cos\frac{π}{8}$,$\sqrt{2+\sqrt{2+\sqrt{2}}}=2cos\frac{π}{16}$,…请从中归纳出第n(n∈N*)个等式:$\underbrace{\sqrt{2+\sqrt{2+…+\sqrt{2}}}}_{n个根号}$=$2cos\frac{π}{{{2^{n+1}}}}$.分析 通过已知的三个等式,找出规律,归纳出第n个等式即可
解答 解:因为:$\sqrt{2}=2cos\frac{π}{4}$,
$\sqrt{2+\sqrt{2}}=2cos\frac{π}{8}$,
$\sqrt{2+\sqrt{2+\sqrt{2}}}=2cos\frac{π}{16}$,
…等式的右边系数是2,角是等比数列,公比为$\frac{1}{2}$角的余弦值,角满足$\frac{π}{{2}^{n+1}}$;
从中归纳出第n(n∈N*)个等式:$\underbrace{\sqrt{2+\sqrt{2+…+\sqrt{2}}}}_{n个根号}$=2cos$\frac{π}{{2}^{n+1}}$.
故答案为:2cos$\frac{π}{{2}^{n+1}}$.
点评 本题考查归纳推理,注意已知表达式的特征是解题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
7.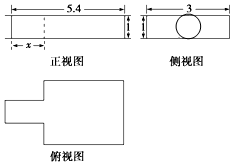 中国古代数学著作《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,一个爱好者根据该标准量器制作了一个几何体模型,该几何体的三视图如图所示(单位:寸),若几何体体积为13.5(立方寸),(π取3),则图中x的为( )
中国古代数学著作《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,一个爱好者根据该标准量器制作了一个几何体模型,该几何体的三视图如图所示(单位:寸),若几何体体积为13.5(立方寸),(π取3),则图中x的为( )
 中国古代数学著作《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,一个爱好者根据该标准量器制作了一个几何体模型,该几何体的三视图如图所示(单位:寸),若几何体体积为13.5(立方寸),(π取3),则图中x的为( )
中国古代数学著作《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,一个爱好者根据该标准量器制作了一个几何体模型,该几何体的三视图如图所示(单位:寸),若几何体体积为13.5(立方寸),(π取3),则图中x的为( )| A. | 2.4 | B. | 1.8 | C. | 1.6 | D. | 1.2 |
8.设函数f(x)=$\left\{\begin{array}{l}{-|lnx|,x>0}\\{{x}^{2}+2x-1,x≤0}\end{array}\right.$,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e-1-2,e2+e-2-2)真假的判断,正确的是( )
| A. | p假q真 | B. | p假q假 | C. | p真q真 | D. | p真q假 |
5.假设你和同桌玩数字游戏,两人各自在心中想一个整数,分别记为x,y,且x,y∈[1,4].如果满足|x-y|≤1,那么就称你和同桌“心灵感应”,则你和同桌“心灵感应”的概率为( )
| A. | $\frac{7}{16}$ | B. | $\frac{5}{8}$ | C. | $\frac{9}{16}$ | D. | $\frac{7}{8}$ |
12.设集合A={x|(x+4)(x-4)>0},B={x|-2<x≤6},则A∩B等于( )
| A. | (-2,4) | B. | (4,-2) | C. | (-4,6) | D. | (4,6] |
1.为了普及环保知识,增强环保意识,某大学从大学理工类专业的A班和文史专业的B班各抽取20名同学参加环保知识测试,统计得到成绩与专业的列联表:
附:参考公式及数据:
①K2统计量:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d);
②独立性检验的临界值表:
( )
| 优秀 | 非优秀 | 总计 | |
| A班 | 14 | 6 | 20 |
| B班 | 7 | 13 | 20 |
| 总计 | 21 | 19 | 40 |
①K2统计量:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d);
②独立性检验的临界值表:
| P(K≥k0) | 0.050 | 0.010 |
| k0 | 3.841 | 6.635 |
| A. | 有99%的把握认为环保知识测试成绩与专业有关 | |
| B. | 有99%的把握认为环保知识测试成绩与专业无关 | |
| C. | 有95%的把握认为环保知识测试成绩与专业无关 | |
| D. | 有95%的把握认为环保知识测试成绩与专业有关 |
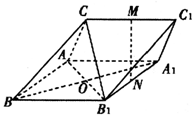 如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.CA⊥CB1,CA=CB1,BA=BC=BB1.
如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.CA⊥CB1,CA=CB1,BA=BC=BB1.