题目内容
已知数列{an}中,a1=1,a2=
,且an+1=
(n=2,3,4,…).Sn为数列{bn}的前n项和,且
4Sn=bnbn+1,b1=2(n=1,2,3,…).
(1)求数列{bn}的通项公式;
(2)设cn=bn•2
+
,求数列{cn}的前n项的和Pn;
(3)证明对一切n∈N*,有
ak2<
.
| 1 |
| 4 |
| (n-1)an |
| n-an |
4Sn=bnbn+1,b1=2(n=1,2,3,…).
(1)求数列{bn}的通项公式;
(2)设cn=bn•2
| 1 |
| 3an |
| 2 |
| 3 |
(3)证明对一切n∈N*,有
| n |
 |
| k=1 |
| 7 |
| 6 |
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列
分析:(1)解:由已知条件推导出b1=2,bn+1-bn-1=4,(n≥2),当n为奇数时,bn=2n;当n为偶数时,bn=2n.由此能求出数列{bn}的通项公式.
(2)由已知,对n≥2有
-
=-(
-
),由此能求出数列{bn}的通项公式.
(3)当k≥2,有ak2=
<
<
(
-
),由此能够证明对一切n∈N*,有
ak2<
.
(2)由已知,对n≥2有
| 1 |
| nan+1 |
| 1 |
| (n-1)an |
| 1 |
| n-1 |
| 1 |
| n |
(3)当k≥2,有ak2=
| 1 |
| (3k-2)2 |
| 1 |
| (3k-4)(3k+4) |
| 1 |
| 3 |
| 1 |
| 3k-4 |
| 1 |
| 3k-1 |
| n |
 |
| k=1 |
| 7 |
| 6 |
解答:
(1)解:由已知b1=2,4Sn=bnbn+1,得b2=4,
4Sn-1=bn-1bn,n≥2,4bn=bn(bn+1-bn-1),
由题意bn≠0,即bn+1-bn-1=4,(n≥2),
当n为奇数时,bn=2n;当n为偶数时,bn=2n.
所以数列{bn}的通项公式为bn=2n,n∈N*.…(4分)
(2)解:由已知,对n≥2有
=
=
-
,
两边同除以n,得
=
-
,
即
-
=-(
-
),
于是,
[
-
]=-
(
-
)=-(1-
),
即
-
=-(1-
),n≥2,
∴
=
-(1-
)=
,
∴an=
,n≥2,又n=1时也成立,
∴an=
,n∈N*.
∴cn=2n•2n,Pn=4+(n-1)•2n+2.…(8分)
(3)当k≥2,有ak2=
<
<
(
-
),
∴n≥2时,有
ak2=1+
ak2<1+
[(
-
)+(
-
)+…+(
-
)]
=1+
(
-
)<1+
=
.
当n=1时,a12=1<
.
故对一切n∈N*,有
ak2<
.…(14分)
4Sn-1=bn-1bn,n≥2,4bn=bn(bn+1-bn-1),
由题意bn≠0,即bn+1-bn-1=4,(n≥2),
当n为奇数时,bn=2n;当n为偶数时,bn=2n.
所以数列{bn}的通项公式为bn=2n,n∈N*.…(4分)
(2)解:由已知,对n≥2有
| 1 |
| an+1 |
| n-an |
| (n-1)an |
| n |
| (n-1)an |
| 1 |
| n-1 |
两边同除以n,得
| 1 |
| nan+1 |
| 1 |
| (n-1)an |
| 1 |
| n(n-1) |
即
| 1 |
| nan+1 |
| 1 |
| (n-1)an |
| 1 |
| n-1 |
| 1 |
| n |
于是,
| n-1 |
 |
| k=2 |
| 1 |
| kak+1 |
| 1 |
| (k-1)ak |
| n-1 |
 |
| k=2 |
| 1 |
| k-1 |
| 1 |
| k |
| 1 |
| n-1 |
即
| 1 |
| (n-1)an |
| 1 |
| a2 |
| 1 |
| n-1 |
∴
| 1 |
| (n-1)an |
| 1 |
| a2 |
| 1 |
| n-1 |
| 3n-2 |
| n-1 |
∴an=
| 1 |
| 3n-2 |
∴an=
| 1 |
| 3n-2 |
∴cn=2n•2n,Pn=4+(n-1)•2n+2.…(8分)
(3)当k≥2,有ak2=
| 1 |
| (3k-2)2 |
| 1 |
| (3k-4)(3k+4) |
| 1 |
| 3 |
| 1 |
| 3k-4 |
| 1 |
| 3k-1 |
∴n≥2时,有
| n |
 |
| k=1 |
| n |
 |
| k=2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 8 |
| 1 |
| 3n-4 |
| 1 |
| 3n-1 |
=1+
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3n-1 |
| 1 |
| 6 |
| 7 |
| 6 |
当n=1时,a12=1<
| 7 |
| 6 |
故对一切n∈N*,有
| n |
 |
| k=1 |
| 7 |
| 6 |
点评:本题考查数列的通项公式的求法,考查数列前n项和的求法,考查不等式的证明,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
设z=x+y,其中x,y满足
,当z的最大值为6时,k的值为( )
|
| A、3 | B、4 | C、5 | D、6 |
已知点O(0,0),A0(0,1),An(6,7),点A1,A2,…,An-1(n∈N,n≥2)是线段A0An的n等分点,则|
+
+…+
+
|等于( )
| OA0 |
| OA1 |
| OAn-1 |
| OAn |
| A、5n | B、10n |
| C、5(n+1) | D、10(n+1) |
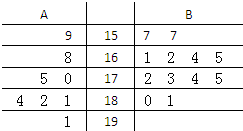 某园艺师培育了两种珍稀树苗A与B,株数分别为8与12,现将这20株树苗的高度编写成如图所示茎叶图(单位:cm).若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.
某园艺师培育了两种珍稀树苗A与B,株数分别为8与12,现将这20株树苗的高度编写成如图所示茎叶图(单位:cm).若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.