��Ŀ����
 ij��ʦ������������ϡ����A��B�������ֱ�Ϊ8��12���ֽ���20������ĸ߶ȱ�д����ͼ��ʾ��Ҷͼ����λ��cm������������175cm���ϣ�����175cm������Ϊ���������á���������175cm���£�������175cm������Ϊ�����������á�����ֻ�С�B�������á��IJſ��Գ��ۣ�
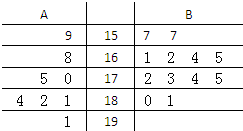
ij��ʦ������������ϡ����A��B�������ֱ�Ϊ8��12���ֽ���20������ĸ߶ȱ�д����ͼ��ʾ��Ҷͼ����λ��cm������������175cm���ϣ�����175cm������Ϊ���������á���������175cm���£�������175cm������Ϊ�����������á�����ֻ�С�B�������á��IJſ��Գ��ۣ���1��������20�����磬����÷ֲ�����ķ����ӡ��������á��͡����������á��й���ȡ5�꣬�ٴ���5������ѡ2�꣬��ô������һ�ꡰ�������á��ĸ����Ƕ��٣�
��2���������С��������á���ѡ2�꣬����ѡ�е����綼�ܳ��۵ĸ��ʣ�
���㣺�ŵ���ͼ�����ʼ��㹫ʽ,�ֲ��������
ר�⣺������ͳ��
��������1�����ݾ�Ҷͼ����֪���������á���8�꣬�����������á�����12�꣬�÷ֲ�����ķ�����������������á��͡����������á������������ö����¼��ĸ��ʣ��������������һ�ꡰ�������á��ĸ��ʣ�
��2�������������ʽ�ô����С��������á���ѡ2����¼���28�����������綼�ܳ��۵Ļ����¼���3�������ݸ��ʹ�ʽ���㼴�ɣ�
��2�������������ʽ�ô����С��������á���ѡ2����¼���28�����������綼�ܳ��۵Ļ����¼���3�������ݸ��ʹ�ʽ���㼴�ɣ�
���
�⣺��1�����ݾ�Ҷͼ����֪���������á���8�꣬�����������á�����12�꣬
�÷ֲ�����ķ�����ȡ��ÿ�걻��ȡ�ĸ�����
=
��
�ӡ��������á��й���ȡ8��
=2�꣬
���������������12��
=3�꣮
�衰�������á�������Ϊ1��2�������������á���3��Ϊa��b��c��
�����еĻ����¼��У�
��1��2������1��a������1��b������1��c����
��2��a������2��b������2��c����
��a��b������a��c����
��b��c������10�֣�
������һ�ꡰ�������á����¼���7��
��������һ�ꡰ�������á��ĸ�����P=
��
��2�������⣬һ����8���������ã�����A��5�꣬B��3�꣬
���п��ܵĻ����¼�����
=
=28����
���綼�ܳ��۵��¼������Ļ����¼�Ϊ
=3����
���������ΪP=
��
�÷ֲ�����ķ�����ȡ��ÿ�걻��ȡ�ĸ�����
| 5 |
| 20 |
| 1 |
| 4 |
�ӡ��������á��й���ȡ8��
| 1 |
| 4 |
���������������12��
| 1 |
| 4 |
�衰�������á�������Ϊ1��2�������������á���3��Ϊa��b��c��
�����еĻ����¼��У�
��1��2������1��a������1��b������1��c����
��2��a������2��b������2��c����
��a��b������a��c����
��b��c������10�֣�
������һ�ꡰ�������á����¼���7��
��������һ�ꡰ�������á��ĸ�����P=
| 7 |
| 10 |
��2�������⣬һ����8���������ã�����A��5�꣬B��3�꣬
���п��ܵĻ����¼�����
| C | 2 8 |
| 8��7 |
| 2��1 |
���綼�ܳ��۵��¼������Ļ����¼�Ϊ
| C | 2 3 |
���������ΪP=
| 3 |
| 28 |
���������⿼���˾�Ҷͼ���ɾ�Ҷͼ�����ݵķ����������˹ŵ���͵ĸ��ʼ��㣬�����Ĺؼ��Ƕ�����Ҷͼ�������е��⣮

��ϰ��ϵ�д�
 �������ϵ�д�
�������ϵ�д�
�����Ŀ
�����ĸ����⣺
��1����һ���ǵ����߷ֱ�ƽ������һ���ǵ����ߣ�������������ȣ�
��2�������� Ϊ������ͬƽ�棬ֱ��a?����ֱ��b?������a�Φ£�b�Φ£�����Φ£�
��3�������� Ϊ������ͬƽ�棬ֱ��m�ͦ���m�ͦ� ����Φ£�
��4�������� Ϊ������ͬƽ�棬ֱ��m�Φ���m�Φ£�����Φ£�
������ȷ���ǣ�������
��1����һ���ǵ����߷ֱ�ƽ������һ���ǵ����ߣ�������������ȣ�
��2�������� Ϊ������ͬƽ�棬ֱ��a?����ֱ��b?������a�Φ£�b�Φ£�����Φ£�
��3�������� Ϊ������ͬƽ�棬ֱ��m�ͦ���m�ͦ� ����Φ£�
��4�������� Ϊ������ͬƽ�棬ֱ��m�Φ���m�Φ£�����Φ£�
������ȷ���ǣ�������
| A����1�� | B����2�� |
| C����3�� | D����4�� |
��a��0��b��0��c��0���в��ȹ�ϵ����������ǣ�������
A��c3+c+1��c2+
| ||||
| B��|a-b|��|a-c|+|b-c| | ||||
C����a+4b=1����
| ||||
| D��ax2+bx+c��0��x��R�� |

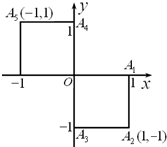 �ס��ҡ���������Ҫѡһ��ȥ�μӳ�����������������ƶ���һ��������Ϊ������ͼ����OΪ��㣬�ٴ�A1��A2��A3��A4��A5����5��������ȡ����ֱ�Ϊ�յ�õ�������������������������������ΪX����X��0���ü�ȥ����X=0������ȥ����X��0���DZ�ȥ��
�ס��ҡ���������Ҫѡһ��ȥ�μӳ�����������������ƶ���һ��������Ϊ������ͼ����OΪ��㣬�ٴ�A1��A2��A3��A4��A5����5��������ȡ����ֱ�Ϊ�յ�õ�������������������������������ΪX����X��0���ü�ȥ����X=0������ȥ����X��0���DZ�ȥ��