题目内容
若实数x,y满足
,则z=|x-3y|的最大值是( )
|
| A、10 | B、8 | C、6 | D、4 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出可行域,可得目标直线的斜率为
,可得经过点A或B时取到最大值,代点计算比较可得答案.
| 1 |
| 3 |
解答:
解:作出
所对应的可行域(如图阴影),
可得目标直线的斜率为
,当直线y=
x经过点A或B时取到最大值,
联立方程组可得A(-2,-2),B(-2,2),
代值计算可得z=|x-3y|的最大值为8
故选:B

|
可得目标直线的斜率为
| 1 |
| 3 |
| 1 |
| 3 |
联立方程组可得A(-2,-2),B(-2,2),
代值计算可得z=|x-3y|的最大值为8
故选:B

点评:本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
如图,空间四边形OABC中,
=
,
=
,
=
,且OM=2MA,BN=NC,则
等于( )
| OA |
| a |
| OB |
| b |
| OC |
| c |
| MN |

A、
| ||||||||||||
B、
| ||||||||||||
C、-
| ||||||||||||
D、
|
在等差数列{an}中an>0,且a1+a2+a3+…+a8=40,则a4•a5的最大值是( )
| A、5 | B、10 |
| C、25 | D、AB=4,50 |
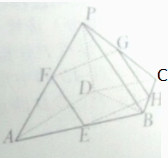 如图,在四棱锥P-ABCD中,若PD=4,DC=DB=3,PB=PC=5,AD⊥DB
如图,在四棱锥P-ABCD中,若PD=4,DC=DB=3,PB=PC=5,AD⊥DB