题目内容

解关于x不等式|2x-1|-|x-2|＜0．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：把要解的不等式等价转化为与之等价的三个不等式组，求出每个不等式组的解集，再取并集，即得所求．
解答： 解：原不等式等价于不等式组①
x≥2
2x-1-(x-2)＜0
，或②
1
2
＜x＜2
2x-1+(x-2)＜0
，或③
x≤
1
2
-(2x-1)+(x-2)＜0
．
不等式组①无解，由②得
1
2
＜x＜1，由③得-1＜x≤
1
2
，
综上得-1＜x＜1，所以，原不等式的解集为{x|-1＜x＜1}．
点评：本题主要考查绝对值不等式的解法，关键是去掉绝对值，化为与之等价的不等式组来解，属于基础题．
练习册系列答案
相关题目
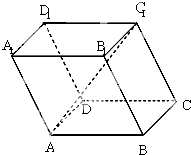已知平行六面体ABCD-A1B1C1D1中，底面ABCD是边长为2的正方形，侧棱AA1的长为2，∠A1AB=∠A1AD=120°．
（1）用基底
AB
，
AD
，
AA1
表示
AC1
；
（2）求对角线AC1的长；
（3）求直线AC1和BB1的夹角的余弦值．
设函数f（x）=ax2-xlnx-（2a-1）x+a-1（a∈R）
（1）当a=0时，求函数f（x）在点P（e，f（e））处的切线方程；
（2）对任意的x∈[1，+∞），函数f（x）≥0恒成立，求实数a的取值范围．
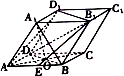如图，四棱柱ABCD-A1B1C1D1的底面ABCD是正方形，O为底面中心，E是AB的中点，A1O=1，A1B=AB=AA1=
2
．
（1）证明：AD1∥平面B1DE；
（2）求三棱柱ABD-A1B1D1的体积．
设函数g（x）=ax2+bx+c（a＞0），且g（1）=-
a
2

（1）求证：函数g（x）有两个零点
（2）设m，n是函数g（x）的两个零点，求|m-n|的取值范围
（3）讨论函数g（x）在区间（0，2）内的零点个数．
若a＞0，求极限：
lim
n→∞
1-2an
1+an
．
一组数据用茎叶图表示如图，则这组数据的中位数是（　　）
A、23B、25C、36D、34
（1）求长轴长为20离心率
3
5
的椭圆的标准方程；
（2）已知椭圆的中心在原点，以坐标轴为对称轴，且经过两点P1(
6
，1)，P2(-
3
，-
2
)，求椭圆方程．
若实数x，y满足
x+3y≤4
y≥x
x≥-2
，则z=|x-3y|的最大值是（　　）
A、10B、8C、6D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网