Question

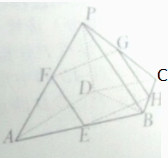如图，在四棱锥P-ABCD中，若PD=4，DC=DB=3，PB=PC=5，AD⊥DB
（1）求证：AD⊥PB；
（2）点E，F，G分别是AB，AP，PC的中点，过E，F，G的平面交BC于H，求线段GH的长．

Answer 1

考点：直线与平面垂直的性质

专题：空间位置关系与距离

分析：（1）△PDC，△PDB中，根据勾股定理得出PD²=PD²+BD²，PC²=PD²+CD²，PD⊥面ABCD，得出AD⊥面PBD，与运用直线平面的垂直求解．
（2）得出EF∥面EFGH，PB∥GH，GH为△PBC的中位线，根据PB=5，得出GH=

5

2

．

解答： 证明：（1）在四棱锥P-ABCD中，若PD=4，DC=DB=3，PB=PC=5，
∵PD²=PD²+BD²，PC²=PD²+CD²，
∴根据勾股定理得出：△PDC，△PDB中都是直角三角形
∴PD⊥BD，PD⊥CD，
∵DB∩CD=D，
∴PD⊥面ABCD，
∵AD?面ABCD，
∴AD⊥PD，
∵AD⊥DB，PD∩DB=D，
∴AD⊥面PBD，
∵PB?面PBD，
∴AD⊥BP
（2）∵点E，F，G分别是AB，AP，PC的中点，
∴△PBA中FE∥PB，
∵EF?面EFGH，PB?面EFGH，
∴PB∥面EFGH，
∵PB?面PBC，GH?面EFGH，面PBC∩面EFGH=GH，
∴PB∥GH，
∵G是PC的中点，
∴GH为△PBC的中位线，
∵PB=5，
∴GH=

5

2

．

点评：本题考查了空间直线平面垂直平行的判定性质的运用，灵活运用直线平面的位置关系求解证明，属于中档题．