题目内容
已知cosα是方程6x2-7x-3=0的根,求
的值.
sin(-α-
| ||||
cos(
|
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:三角函数的求值
分析:求出方程的根,利用诱导公式化简所求表达式,然后通过同角三角函数的基本关系式求解即可.
解答:
解:由cosα是方程6x2-7x-3=0的根,可得
cosα=-
或cosα=
(舍),…(3分)
=
=
=-tanα,…(9分)
由cosα=-
可知α是第二象限或者第三象限角.
所以tanα=2
或-2
即所求式子的值为±2
. …(12分)
cosα=-
| 1 |
| 3 |
| 3 |
| 2 |
sin(-α-
| ||||
cos(
|
=
sin(α+
| ||||
| -sinα•sinα |
=
| cosα•cosα•tan3α |
| -sinα•sinα |
=-tanα,…(9分)
由cosα=-
| 1 |
| 3 |
所以tanα=2
| 2 |
| 2 |
即所求式子的值为±2
| 2 |
点评:本题考查诱导公式的应用,函数的零点的求法,同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
相关题目
已知
=(2,3),
=(-4,7),则向量
在
方向上设射影的数量为( )
| a |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若实数x,y满足
,则z=|x-3y|的最大值是( )
|
| A、10 | B、8 | C、6 | D、4 |
设余弦曲线y=-
cosx上一点P,以点P为切点的切线为直线l,则直线l的倾斜角的范围是( )
| 3 |
A、[0,
| ||||||
B、[0,
| ||||||
| C、[0,π) | ||||||
D、[
|
x1、x2.是方程x2-(a-2)x+(a2+3a+5)=0(a为实数)的二实根,则x12+x12的最大值为( )
| A、20 | B、19 | C、18 | D、不存在 |
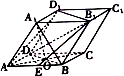 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,E是AB的中点,A1O=1,A1B=AB=AA1=
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,E是AB的中点,A1O=1,A1B=AB=AA1=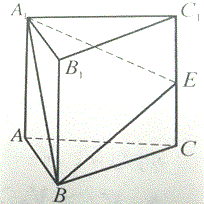 正三棱柱ABC-A1B1C1中,所有棱长都是4,E是CC1的中点.
正三棱柱ABC-A1B1C1中,所有棱长都是4,E是CC1的中点.