题目内容
以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知直线l的参数方程是
(t为参数),曲线C的极坐标方程是ρsin2θ=3cosθ,则直线l被曲线C截得的弦长为( )
|
A、
| ||||
| B、6 | ||||
| C、12 | ||||
D、7
|
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:先将参数方程、极坐标方程化为直角坐标方程,判断出直线l过抛物线y2=3x焦点F(
,0),设出交点坐标联立方程消去y后,再由韦达定理求出x1+x2,代入焦点弦公式求值即可.
| 3 |
| 4 |
解答:
解:由
(t为参数)得,直线l普通方程是:y=
x-
,
由ρsin2θ=3cosθ得,ρ2sin2θ=3ρcosθ,即y2=3x,
则抛物线y2=3x的焦点是F(
,0),
所以直线l过抛物线y2=3x焦点F(
,0),
设直线l与曲线C交于点A(x1、y1)、B(x2、y2),
由
得,16x2-168x+9=0,
所以△>0,且x1+x2=
,
所以|AB|=x1+x2+p=
+
=12,
故选:C.
|
| ||
| 3 |
| ||
| 4 |
由ρsin2θ=3cosθ得,ρ2sin2θ=3ρcosθ,即y2=3x,
则抛物线y2=3x的焦点是F(
| 3 |
| 4 |
所以直线l过抛物线y2=3x焦点F(
| 3 |
| 4 |
设直线l与曲线C交于点A(x1、y1)、B(x2、y2),
由
|
所以△>0,且x1+x2=
| 168 |
| 16 |
所以|AB|=x1+x2+p=
| 168 |
| 16 |
| 3 |
| 2 |
故选:C.
点评:本题考查参数方程、极坐标方程化为直角坐标方程,以及直线与抛物线相交时焦点弦的求法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
集合M={(x,y)|x=
},N={(x,y)|y=x+m},若M∩N的子集恰有4个,则M的取值范围是( )
| 1-y2 |
A、[-
| ||||
B、[1,
| ||||
C、[-1,
| ||||
D、(-
|
设函数f(x)=
(a>0,x∈R),已知区间A=[
,
](m<n),集合B={f(x)|m≤x≤n},则使得A=B成立的实数a的取值范围是( )
| 2ax3 |
| 1+|x| |
| m2 |
| 2 |
| n2 |
| 2 |
A、a>
| ||
B、a≤
| ||
C、0<a≤
| ||
D、0<a<
|
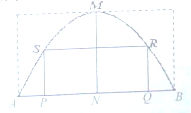 如图是一块外轮廓线(A,B间的曲线部分)为抛物线的钢板,MN为抛物线的对称轴,A,B是抛物线上关于MN对称的两点,其中AB=2,MN=1,先要将其割成矩形PQRS,使矩形的两个顶点P,Q落在线段AB上,另两个顶点R,S落在抛物线上.(1)建立适当的直角坐标系,求出这一抛物线的方程;
如图是一块外轮廓线(A,B间的曲线部分)为抛物线的钢板,MN为抛物线的对称轴,A,B是抛物线上关于MN对称的两点,其中AB=2,MN=1,先要将其割成矩形PQRS,使矩形的两个顶点P,Q落在线段AB上,另两个顶点R,S落在抛物线上.(1)建立适当的直角坐标系,求出这一抛物线的方程;