Question

集合M={（x，y）|x=

1-y2

}，N={（x，y）|y=x+m}，若M∩N的子集恰有4个，则M的取值范围是（　　）

• A、[-

  2

  ，

  2

  ]
• B、[1，

  2

  ）
• C、[-1，

  2

  ]
• D、（-

  2

  ，-1]

Answer 1

考点：子集与真子集

专题：集合

分析：M∩N的子集恰有4个，可知M∩N的元素只有2个，即直线与半圆相交．利用数形结合即可得出．

解答： 解：由x=

1-y2

，化为x²+y²=1（x≥0），表示半圆．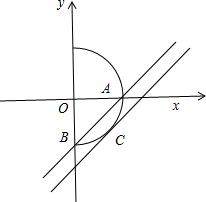
当直线y=x+m与上述半圆相切时，联立

y=x+m x2+y2=1

，化为2x²+2mx+m²-1=0，
令△=4m²-8（m²-1）=0，
解得m=±

2

，取m=-

2

．
当直线y=x+m经过点A（1，0），B（0，-1）时，m=-1，此时直线与半圆相交于两点．
∵M∩N的子集恰有4个，
∴M∩N的元素只有2个，即直线与半圆相交．
∴-

2

＜m≤-1．
故选：D．

点评：本题考查了集合的性质、直线与半圆相交问题、数形结合思想方法，考查了推理能力与计算能力，属于基础题．