题目内容
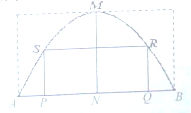如图是一块外轮廓线（A，B间的曲线部分）为抛物线的钢板，MN为抛物线的对称轴，A，B是抛物线上关于MN对称的两点，其中AB=2，MN=1，先要将其割成矩形PQRS，使矩形的两个顶点P，Q落在线段AB上，另两个顶点R，S落在抛物线上．（1）建立适当的直角坐标系，求出这一抛物线的方程；（2）求矩形PQRS面积的最大值．
考点：导数在最大值、最小值问题中的应用,抛物线的应用
专题：计算题,应用题,作图题,导数的综合应用,圆锥曲线的定义、性质与方程
分析：（1）以顶点M为原点，抛物线的对称轴为y轴，建立直角坐标系，从而写出点的坐标，代入方程求方程；
（2）设R（x，-x2），Q（x，-1），从而写出面积S（x）=2x（1-x2）=2x-2x3，（0＜x＜1）；求导，由导数的正负确定函数的单调性，从而求最值．
（2）设R（x，-x2），Q（x，-1），从而写出面积S（x）=2x（1-x2）=2x-2x3，（0＜x＜1）；求导，由导数的正负确定函数的单调性，从而求最值．
解答：
解：（1）如图，以顶点M为原点，抛物线的对称轴为y轴，
建立直角坐标系，则B（1，-1），设抛物线方程为x2=-2py，
将B（1，-1）代入得，
P=
，
即抛物线方程为y=-x2（-1≤x≤1）；
（2）设R（x，-x2），Q（x，-1），
则矩形PQRS的长宽分别是2x，1-x2，
其面积为S（x）=2x（1-x2）=2x-2x3，（0＜x＜1）；
S′（x）=2-6x2，
令S′（x）=2-6x2=0解得，x=
；
列表如下，
则当x=
时，S（x）有最大值
；
故矩形PQRS的面积最大值为
．
解：（1）如图，以顶点M为原点，抛物线的对称轴为y轴，建立直角坐标系，则B（1，-1），设抛物线方程为x2=-2py，
将B（1，-1）代入得，
P=
| 1 |
| 2 |
即抛物线方程为y=-x2（-1≤x≤1）；
（2）设R（x，-x2），Q（x，-1），
则矩形PQRS的长宽分别是2x，1-x2，
其面积为S（x）=2x（1-x2）=2x-2x3，（0＜x＜1）；
S′（x）=2-6x2，
令S′（x）=2-6x2=0解得，x=
| ||
| 3 |
列表如下，
| x | （0，
|
| （
| ||||||||||||
| S′（x） | + | 0 | - | ||||||||||||
| S（x） | 上升 |
| 下降 |
| ||
| 3 |
| 4 |
| 9 |
| 3 |
故矩形PQRS的面积最大值为
| 4 |
| 9 |
| 3 |
点评：本题考查了圆锥曲线的应用，导数的综合应用及作图能力，同时考查了函数在实际问题中的应用，属于难题．
练习册系列答案
应用题作业本系列答案
相关题目
数列{an}满足an+1=
己知一个几何体的三视图如图．则该几何体的表面积为（ ）A、6+2
| ||||
B、2+2
| ||||
C、6+2
| ||||
D、2+2
|
以平面直角坐标系的原点为极点，x轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位，已知直线l的参数方程是
（t为参数），曲线C的极坐标方程是ρsin2θ=3cosθ，则直线l被曲线C截得的弦长为（ ）
|
A、
| ||||
| B、6 | ||||
| C、12 | ||||
D、7
|
已知点M（a，b）（ab≠0）是圆x2+y2=r2内一点，直线g是以M为中点的弦所在直线，直线l的方程为bx-ay+r2=0，则（ ）
| A、l⊥g，且l与圆相离 |
| B、l⊥g，且l与圆相切 |
| C、l∥g，且l与圆相交 |
| D、l∥g，且l与圆相离 |