题目内容
已知数列{an}{bn}的每一项都是正数,a1=4,b1=8且an,bn,an+1成等差数列,an,bn,an+1,bn+1成等比数列(n∈N*)
(Ⅰ)求a2,b2;
(Ⅱ)求数列{an}{bn}的通项公式;
(Ⅲ)证明:对一切正整数n,都有
+
+…+
<
.
(Ⅰ)求a2,b2;
(Ⅱ)求数列{an}{bn}的通项公式;
(Ⅲ)证明:对一切正整数n,都有
| 1 |
| a1-1 |
| 1 |
| a2-1 |
| 1 |
| an-1 |
| 2 |
| 3 |
考点:数列与不等式的综合
专题:综合题,等差数列与等比数列
分析:(Ⅰ)由题意得到2b1=a1+a2,a22=b1b2,代入已知可得a2,b2的值;
(Ⅱ)由已知得2bn=an+an+1,an+12=bnbn+1,进一步得到当n≥2时an=
,三式联立即可得到数列{
}是等差数列,求出其通项后可得数列{bn}的通项公式,结合an=
得到数列{an}的通项公式;
(Ⅲ)把{an}的通项公式代入
并整理,放大后列项,代入
+
+…+
证得答案.
(Ⅱ)由已知得2bn=an+an+1,an+12=bnbn+1,进一步得到当n≥2时an=
| bn-1bn |
| bn |
| bn-1bn |
(Ⅲ)把{an}的通项公式代入
| 1 |
| an-1 |
| 1 |
| a1-1 |
| 1 |
| a2-1 |
| 1 |
| an-1 |
解答:
解:(Ⅰ)由an,bn,an+1成等差数列,an,bn,an+1,bn+1成等比数列,
得:2b1=a1+a2,a22=b1b2,
∵a1=4,b1=8,
∴a2=2b1-a1=12,
b2=
=18;
(Ⅱ)∵an,bn,an+1成等差数列,
∴2bn=an+an+1…①.
∵bn,an+1,bn+1成等比数列,
∴an+12=bnbn+1,
∵数列{an},{bn}的每一项都是正数,
∴an+1=
…②.
于是当n≥2时,an=
…③.
将②、③代入①式,可得2
=
+
,
因此数列{
}是首项为2
,公差为
的等差数列.
∴
=2
+
(n-1)=
(n+1),
则bn=2(n+1)2.
由③式,可得当n≥2时,an=
=2n(n+1).
当n=1时,a1=4,满足该式子,
∴对一切正整数n,都有an=2n(n+1);
(Ⅲ)证明:由(2)可知,所证明的不等式为
+
+
+…+
<
.
∵
=
<
=
=
(
-
) (n≥2),
∴当n≥2时,
+
+…+
<
+
(
-
+
-
+
-
+…+
-
)<
+
(1+
+
)=
<
.
当n=1时,
<
.
综上所述,对一切正整数n,有
+
+…+
<
.
得:2b1=a1+a2,a22=b1b2,
∵a1=4,b1=8,
∴a2=2b1-a1=12,
b2=
| a22 |
| b1 |
(Ⅱ)∵an,bn,an+1成等差数列,
∴2bn=an+an+1…①.
∵bn,an+1,bn+1成等比数列,
∴an+12=bnbn+1,
∵数列{an},{bn}的每一项都是正数,
∴an+1=
| bnbn+1 |
于是当n≥2时,an=
| bn-1bn |
将②、③代入①式,可得2
| bn |
| bn-1 |
| bn+1 |
因此数列{
| bn |
| 2 |
| 2 |
∴
| bn |
| 2 |
| 2 |
| 2 |
则bn=2(n+1)2.
由③式,可得当n≥2时,an=
| bn-1bn |
当n=1时,a1=4,满足该式子,
∴对一切正整数n,都有an=2n(n+1);
(Ⅲ)证明:由(2)可知,所证明的不等式为
| 1 |
| 3 |
| 1 |
| 11 |
| 1 |
| 23 |
| 1 |
| 2n2+2n-1 |
| 2 |
| 3 |
∵
| 1 |
| 2n2+2n-1 |
| 1 |
| 2 |
| 1 | ||
n2+n-
|
| 1 |
| 2 |
| 1 |
| n2+n-2 |
| 1 |
| 2 |
| 1 |
| (n-1)(n+2) |
| 1 |
| 6 |
| 1 |
| n-1 |
| 1 |
| n+2 |
∴当n≥2时,
| 1 |
| a1-1 |
| 1 |
| a2-1 |
| 1 |
| an-1 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 1 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| n-1 |
| 1 |
| n+2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 23 |
| 36 |
| 2 |
| 3 |
当n=1时,
| 1 |
| 3 |
| 2 |
| 3 |
综上所述,对一切正整数n,有
| 1 |
| a1-1 |
| 1 |
| a2-1 |
| 1 |
| an-1 |
| 2 |
| 3 |
点评:本题是数列与不等式的综合题,考查了等差数列与等比数列的性质,训练了利用裂项相消法求数列的和,考查了放缩法证明不等式,属难题.

练习册系列答案
相关题目
已知平面向量
=(2,3),
=(x,y),
-
=(1,7),则x,y的值分别是( )
| a |
| b |
| b |
| 2a |
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
已知边长为1的正三角形ABC,D是BC的中点,E是AC上一点且AE=2EC.则
•
=( )
| AD |
| BE |
A、
| ||
B、-
| ||
| C、0 | ||
| D、4 |
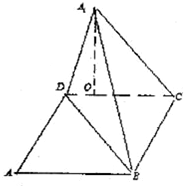 如图,矩形ABCD中,AB=10,BC=6,沿对角线BD吧△ABD折起到△A1BD的位置,使A1在平面BCD上的射影O恰好在CD上.
如图,矩形ABCD中,AB=10,BC=6,沿对角线BD吧△ABD折起到△A1BD的位置,使A1在平面BCD上的射影O恰好在CD上.