题目内容
已知函数f0(x)=
(x>0),设fn(x)为fn-1(x)的导数,n∈N*.
(1)求2f1(
)+
f2(
)的值;
(2)证明:对任意n∈N*,等式|nfn-1(
)+
fn(
)|=
都成立.
| sinx |
| x |
(1)求2f1(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
(2)证明:对任意n∈N*,等式|nfn-1(
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
考点:三角函数中的恒等变换应用,导数的运算
专题:函数的性质及应用,三角函数的求值
分析:(1)由于求两个函数的相除的导数比较麻烦,根据条件和结论先将原函数化为:xf0(x)=sinx,然后两边求导后根据条件两边再求导得:2f1(x)+xf2(x)=-sinx,把x=
代入式子求值;
(2)由(1)得,f0(x)+xf1(x)=cosx和2f1(x)+xf2(x)=-sinx,利用相同的方法再对所得的式子两边再求导,并利用诱导公式对所得式子进行化简、归纳,再进行猜想得到等式,用数学归纳法进行证明等式成立,主要利用假设的条件、诱导公式、求导公式以及题意进行证明,最后再把x=
代入所给的式子求解验证.
| π |
| 2 |
(2)由(1)得,f0(x)+xf1(x)=cosx和2f1(x)+xf2(x)=-sinx,利用相同的方法再对所得的式子两边再求导,并利用诱导公式对所得式子进行化简、归纳,再进行猜想得到等式,用数学归纳法进行证明等式成立,主要利用假设的条件、诱导公式、求导公式以及题意进行证明,最后再把x=
| π |
| 4 |
解答:
解:(1)∵f0(x)=
,∴xf0(x)=sinx,
则两边求导,[xf0(x)]′=(sinx)′,
∵fn(x)为fn-1(x)的导数,n∈N*,
∴f0(x)+xf1(x)=cosx,
两边再同时求导得,2f1(x)+xf2(x)=-sinx,
将x=
代入上式得,2f1(
)+
f2(
)=-1,
(2)由(1)得,f0(x)+xf1(x)=cosx=sin(x+
),
恒成立两边再同时求导得,2f1(x)+xf2(x)=-sinx=sin(x+π),
再对上式两边同时求导得,3f2(x)+xf3(x)=-cosx=sin(x+
),
同理可得,两边再同时求导得,4f3(x)+xf4(x)=sinx=sin(x+2π),
猜想得,nfn-1(x)+xfn(x)=sin(x+
)对任意n∈N*恒成立,
下面用数学归纳法进行证明等式成立:
①当n=1时,f0(x)+xf1(x)=cosx=sin(x+
)成立,则上式成立;
②假设n=k(k>1且k∈N*)时等式成立,即kfk-1(x)+xfk(x)=sin(x+
),
∵[kfk-1(x)+xfk(x)]′=kfk-1′(x)+fk(x)+xfk′(x)
=(k+1)fk(x)+xfk+1(x)
又[sin(x+
)]′=cos(x+
)•(x+
)′
=cos(x+
)=sin(
+x+
)=sin[x+
],
∴那么n=k+1(k>1且k∈N*)时.等式(k+1)fk(x)+xfk+1(x)=sin[x+
]也成立,
由①②得,nfn-1(x)+xfn(x)=sin(x+
)对任意n∈N*恒成立,
令x=
代入上式得,nfn-1(
)+
fn(
)=sin(
+
)=±cos
=±
,
所以,对任意n∈N*,等式|nfn-1(
)+
fn(
)|=
都成立.
| sinx |
| x |
则两边求导,[xf0(x)]′=(sinx)′,
∵fn(x)为fn-1(x)的导数,n∈N*,
∴f0(x)+xf1(x)=cosx,
两边再同时求导得,2f1(x)+xf2(x)=-sinx,
将x=
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
(2)由(1)得,f0(x)+xf1(x)=cosx=sin(x+
| π |
| 2 |
恒成立两边再同时求导得,2f1(x)+xf2(x)=-sinx=sin(x+π),
再对上式两边同时求导得,3f2(x)+xf3(x)=-cosx=sin(x+
| 3π |
| 2 |
同理可得,两边再同时求导得,4f3(x)+xf4(x)=sinx=sin(x+2π),
猜想得,nfn-1(x)+xfn(x)=sin(x+
| nπ |
| 2 |
下面用数学归纳法进行证明等式成立:
①当n=1时,f0(x)+xf1(x)=cosx=sin(x+
| π |
| 2 |
②假设n=k(k>1且k∈N*)时等式成立,即kfk-1(x)+xfk(x)=sin(x+
| kπ |
| 2 |
∵[kfk-1(x)+xfk(x)]′=kfk-1′(x)+fk(x)+xfk′(x)
=(k+1)fk(x)+xfk+1(x)
又[sin(x+
| kπ |
| 2 |
| kπ |
| 2 |
| kπ |
| 2 |
=cos(x+
| kπ |
| 2 |
| π |
| 2 |
| kπ |
| 2 |
| (k+1)π |
| 2 |
∴那么n=k+1(k>1且k∈N*)时.等式(k+1)fk(x)+xfk+1(x)=sin[x+
| (k+1)π |
| 2 |
由①②得,nfn-1(x)+xfn(x)=sin(x+
| nπ |
| 2 |
令x=
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| nπ |
| 2 |
| π |
| 4 |
| ||
| 2 |
所以,对任意n∈N*,等式|nfn-1(
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
点评:本题考查了三角函数、复合函数的求导数公式和法则、诱导公式,以及数学归纳法证明命题、转化思想等,本题设计巧妙,题型新颖,立意深刻,是一道不可多得的好题,难度很大,考查了学生观察问题、分析问题、解决问题的能力,以及逻辑思维能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
与双曲线2y2-x2=4焦距不同的是( )
| A、2x2-y2=4 |
| B、y2-x2=3 |
| C、x2+4y2=8 |
| D、2y2+x2=6 |
已知函数f(x)是定义在R上的奇函数,对任意x,y∈R,x+y≠0,都有
>0,若x>2y,则( )
| f(x)+f(y) |
| x+y |
| A、f(x)>f(2y) |
| B、f(x)≥f(2y) |
| C、f(x)<f(2y) |
| D、f(x)≤f(2y) |
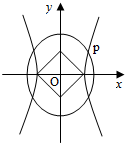 如图,O为坐标原点,双曲线C1:
如图,O为坐标原点,双曲线C1: