题目内容
已知边长为1的正三角形ABC，D是BC的中点，E是AC上一点且AE=2EC．则
•
=（ ）
| AD |
| BE |
A、
| ||
B、-
| ||
| C、0 | ||
| D、4 |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：先由平行四边形法则、三角形法则得
=
(
+
)，
=
-
=
-
，再由数量积运算性质可求．
| AD |
| 1 |
| 2 |
| AB |
| AC |
| BE |
| AE |
| AB |
| 2 |
| 3 |
| AC |
| AB |
解答：
解：∵ABC是边长为1的正三角形，
∴
•
=1×1×cos60°=
，
又
=
(
+
)，
=
-
=
-
，
∴
•
=
(
+
)•(
-
)=-
•
-
2+
2=-
-
+
=-
，
故选B．
∴
| AB |
| AC |
| 1 |
| 2 |
又
| AD |
| 1 |
| 2 |
| AB |
| AC |
| BE |
| AE |
| AB |
| 2 |
| 3 |
| AC |
| AB |
∴
| AD |
| BE |
| 1 |
| 2 |
| AB |
| AC |
| 2 |
| 3 |
| AC |
| AB |
| 1 |
| 6 |
| AB |
| AC |
| 1 |
| 2 |
| AB |
| 1 |
| 3 |
| AC |
| 1 |
| 12 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
故选B．
点评：本题考查平面向量基本定理、数量积运算性质，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
复数z=
的共轭复数对应的点在（ ）
| 2 |
| -1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知复数z=
，则复数z的共轭复数在复平面内对应的点在（ ）
| 2+i |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设i是虚数单位，
是复数z=
+
i的共轭复数，则z2•
=（ ）
. |
| z |
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
已知函数f（x）是定义在R上的奇函数，对任意x，y∈R，x+y≠0，都有
＞0，若x＞2y，则（ ）
| f(x)+f(y) |
| x+y |
| A、f（x）＞f（2y） |
| B、f（x）≥f（2y） |
| C、f（x）＜f（2y） |
| D、f（x）≤f（2y） |
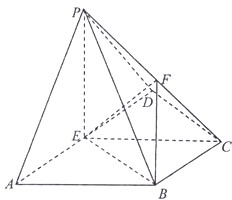如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，ABCD是梯形，BC∥AD，E，F分别是AD，PC的中点，△ABE，△BEC，△ECD都是边长为1的等边三角形．