题目内容
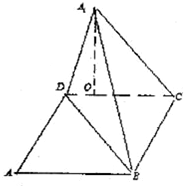如图，矩形ABCD中，AB=10，BC=6，沿对角线BD吧△ABD折起到△A1BD的位置，使A1在平面BCD上的射影O恰好在CD上．（1）求证：BC⊥A1D；
（2）求直线A1C与平面A1BD所成角的余弦值．
考点：直线与平面所成的角,直线与平面垂直的性质
专题：空间位置关系与距离
分析：（1）由已知条件推导出A1O⊥平面BCD，BC⊥A1O，从而得到BC⊥平面A1CD，由此能证明BC⊥A1B．
（2）由（1）得BC⊥A1D，结合A1D⊥A1B和线面垂直的判定定理可得A1D⊥平面A1BC，进而平面A1DB⊥平面A1BC，过C作CE⊥A1B于E，∠CA1E即为直线A1C与平面A1BD所成角，解三角形可得答案．
（2）由（1）得BC⊥A1D，结合A1D⊥A1B和线面垂直的判定定理可得A1D⊥平面A1BC，进而平面A1DB⊥平面A1BC，过C作CE⊥A1B于E，∠CA1E即为直线A1C与平面A1BD所成角，解三角形可得答案．
解答：
证明：（1）∵A1在平面BCD上的射影O在CD上，
∴A1O⊥平面BCD，
又∵BC?平面BCD，∴BC⊥A1O，
又∵BC⊥CO，A1O∩CO=O，∴BC⊥平面A1CD，
又∵A1D?平面A1CD，
∴BC⊥A1D．
解：（2）由（1）得BC⊥A1D，
又∵A1D⊥A1B，A1B∩BC=B，A1B，BC?平面A1BC，
∴A1D⊥平面A1BC，
又∵A1D?平面A1DB，
∴平面A1DB⊥平面A1BC，
过C作CE⊥A1B于E，
则CE⊥平面A1BD，
∴∠CA1E即为直线A1C与平面A1BD所成角，
∴sin∠CA1E=
=
，
∴cos∠CA1E=
．
∴A1O⊥平面BCD，
又∵BC?平面BCD，∴BC⊥A1O，
又∵BC⊥CO，A1O∩CO=O，∴BC⊥平面A1CD，
又∵A1D?平面A1CD，
∴BC⊥A1D．
解：（2）由（1）得BC⊥A1D，
又∵A1D⊥A1B，A1B∩BC=B，A1B，BC?平面A1BC，
∴A1D⊥平面A1BC，
又∵A1D?平面A1DB，
∴平面A1DB⊥平面A1BC，
过C作CE⊥A1B于E，
则CE⊥平面A1BD，
∴∠CA1E即为直线A1C与平面A1BD所成角，
∴sin∠CA1E=
| BC |
| A1B |
| 3 |
| 5 |
∴cos∠CA1E=
| 4 |
| 5 |
点评：本题考查异面直线垂直的证明，考查线面夹角的余弦值的求法，考查运算推恒能力，解题时要注意空间思维能力的培养．
练习册系列答案
相关题目
设i是虚数单位，
是复数z=
+
i的共轭复数，则z2•
=（ ）
. |
| z |
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
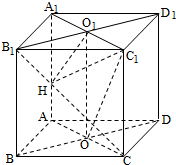如图，四棱柱ABCD-A1B1C1D1的所有棱长都相等，AC∩BD=O，A1C1∩B1D1=O1，四边形ACC1A1和四边形BDD1B1均为矩形．
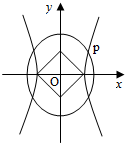如图，O为坐标原点，双曲线C1：