题目内容
已知各项为正数的等差数列{an}满足a3•a7=32,a2+a8=12,且bn=2-an(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设cn=an+bn,求数列{cn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设cn=an+bn,求数列{cn}的前n项和Sn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)依题意,可得a2+a8=a3+a7=12,解方程组
,利用an>0,可求得d=1,从而可得数列{an}的通项公式;
(Ⅱ)由于cn=an+bn=(n+1)+(
)n+1,利用分组求和即可求得数列{cn}的前n项和Sn.
|
(Ⅱ)由于cn=an+bn=(n+1)+(
| 1 |
| 2 |
解答:
解:(Ⅰ)∵{an} 是等差数列,∴a2+a8=a3+a7=12,
⇒
,或
,…(4分)
又an>0,∴
,
解得d=1,
∴an=a3+(n-3)d=4+(n-3)×1=n+1.…(6分)
(Ⅱ)∵bn=2-an=(
)n+1,
∴cn=an+bn=(n+1)+(
)n+1,
∴Sn=(a1+b1)+(a2+b2)+…+(an+bn)
=(a1+a2+…+an)+(b1+b2+…+bn) …(9分)
=[2+3+…+(n+1)]+[(
)2+(
)3+…+(
)n+1]
=
+
=
+
.…(12分)
|
|
|
又an>0,∴
|
解得d=1,
∴an=a3+(n-3)d=4+(n-3)×1=n+1.…(6分)
(Ⅱ)∵bn=2-an=(
| 1 |
| 2 |
∴cn=an+bn=(n+1)+(
| 1 |
| 2 |
∴Sn=(a1+b1)+(a2+b2)+…+(an+bn)
=(a1+a2+…+an)+(b1+b2+…+bn) …(9分)
=[2+3+…+(n+1)]+[(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| n(2+n+1) |
| 2 |
(
| ||||
1-(
|
=
| n(n+3) |
| 2 |
| 2n-1 |
| 2n+1 |
点评:本题考查等差数列的性质,着重考查分组求和法的应用,考查方程思想与等价转化思想的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=log5(x2+1),x∈[2,+∞)的反函数是( )
A、g(x)=
| ||
B、g(x)=
| ||
C、g(x)=
| ||
D、g(x)=
|
设i是虚数单位,
是复数z=
+
i的共轭复数,则z2•
=( )
. |
| z |
| 1 |
| 2 |
| ||
| 2 |
. |
| z |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
已知函数f(x)是定义在R上的奇函数,对任意x,y∈R,x+y≠0,都有
>0,若x>2y,则( )
| f(x)+f(y) |
| x+y |
| A、f(x)>f(2y) |
| B、f(x)≥f(2y) |
| C、f(x)<f(2y) |
| D、f(x)≤f(2y) |
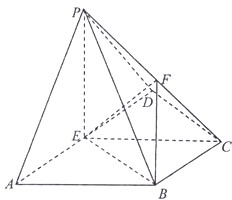 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.