题目内容
函数f（x）=5-cos（4x+
）的最大值是（ ）
| π |
| 9 |
| A、1 | B、-1 | C、4 | D、6 |
考点：余弦函数的图象
专题：三角函数的图像与性质
分析：根据余弦函数的性质即可得到结论．
解答：
解：由余弦函数的性质可知当cos（4x+
）=-1时，函数f（x）取得最大值，为5-（-1）=6，
故选：D．
| π |
| 9 |
故选：D．
点评：本题主要考查三角函数的最值求法，利用余弦函数的有界性和性质是解决本题的关键，比较基础．
练习册系列答案
相关题目
下列函数是偶函数，且在[0，1]上单调递增的是（ ）
A、y=cos（x+
| ||
| B、y=1-2cos22x | ||
| C、y=-x2 | ||
| D、y=|sin（π+x）| |
已知a∈R，若函数f（x）=x2-|2x-a|有四个零点，则关于x的方程ax2+2x+1=0的实数根的个数为（ ）
| A、2个 | B、1个 |
| C、0个 | D、与a的取值有关 |
△ABC中，tanC=
，AB=2
，AC=6，则∠B=（ ）
| ||
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
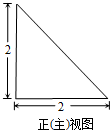某三棱锥的三视图是三个全等的等腰直角三角形，且正（主）视图如图所示，则此三棱锥的表面积为（ ）A、6+2
| ||||
B、4+4
| ||||
C、6+4
| ||||
D、4+4
|
tan19°+tan41°+
tan19°tan41°的值为（ ）
| 3 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、-
|