题目内容
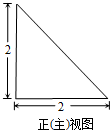 某三棱锥的三视图是三个全等的等腰直角三角形,且正(主)视图如图所示,则此三棱锥的表面积为( )
某三棱锥的三视图是三个全等的等腰直角三角形,且正(主)视图如图所示,则此三棱锥的表面积为( )A、6+2
| ||||
B、4+4
| ||||
C、6+4
| ||||
D、4+4
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:结合直观图判断各面的形状,根据三视图的数据求相关几何量的数据,把数据代入三角形面积公式计算.
解答:
 解:由三棱锥的三视图是三个全等的等腰直角三角形,其直观图有两种情况,当直观图如图所示时:BC⊥AC,SA=AC=BC=2,SA⊥平面ABC,
解:由三棱锥的三视图是三个全等的等腰直角三角形,其直观图有两种情况,当直观图如图所示时:BC⊥AC,SA=AC=BC=2,SA⊥平面ABC,
∴AB=2
,SC=2
,各面都是直角三角形,
∴几何体的表面积S=2×
×2×2+2×
×2
×2=4+4
.
当AB⊥AC,AB=AC=SA=2,AD=
,SD=
,BC=2
,
∴几何体的表面积S=3×
×2×2+
×2
×
=6+2
.

故选:D.
 解:由三棱锥的三视图是三个全等的等腰直角三角形,其直观图有两种情况,当直观图如图所示时:BC⊥AC,SA=AC=BC=2,SA⊥平面ABC,
解:由三棱锥的三视图是三个全等的等腰直角三角形,其直观图有两种情况,当直观图如图所示时:BC⊥AC,SA=AC=BC=2,SA⊥平面ABC,∴AB=2
| 2 |
| 2 |
∴几何体的表面积S=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
当AB⊥AC,AB=AC=SA=2,AD=
| 2 |
| 6 |
| 2 |
∴几何体的表面积S=3×
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 6 |
| 3 |

故选:D.
点评:本题考查了由三视图求几何体的表面积,根据三视图判断几何体的结构特征及相关几何量的数据是解答本题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
设a=
(3x2-2x)dx,则(ax2-
)6的展开式中的第4项为( )
| ∫ | 2 1 |
| 1 |
| x |
| A、-1280x3 |
| B、-1280 |
| C、240 |
| D、-240 |
已知全集U=R,集合A=﹛x|x-2>0﹜,B=﹛x|x|≤1﹜.则(∁UA)∪B=( )
| A、{x|-1≤x≤1} |
| B、{x|-1≤x≤1或x>2} |
| C、{x|-1≤x≤2} |
| D、{x|x≤2} |
下列赋值语句正确的是( )
| A、a-b=2 | B、5=a |
| C、a=b=4 | D、a=a+2 |
函数f(x)=5-cos(4x+
)的最大值是( )
| π |
| 9 |
| A、1 | B、-1 | C、4 | D、6 |
执行如图所示的程序框图,若输入n=2014,则输出的S=( )


A、
| ||
B、
| ||
C、
| ||
D、
|