题目内容
13.已知角A为锐角,则f(A)=$\frac{[cos(π-2A)-1]sin(π+\frac{A}{2})sin(\frac{π}{2}-\frac{A}{2})}{si{n}^{2}(\frac{π}{2}-\frac{A}{2})-si{n}^{2}(π-\frac{A}{2})}$+cos2A的最大值为( )| A. | $\frac{\sqrt{2}+1}{2}$ | B. | $\frac{\sqrt{2}-1}{2}$ | C. | $\frac{\sqrt{3}-1}{4}$ | D. | $\frac{\sqrt{3}+1}{4}$ |
分析 由条件利用三角恒等变换化简f(A)的解析式,再利用正弦函数的值域,求得f(A)的最大值.
解答 解:∵角A为锐角,则f(A)=$\frac{[cos(π-2A)-1]sin(π+\frac{A}{2})sin(\frac{π}{2}-\frac{A}{2})}{si{n}^{2}(\frac{π}{2}-\frac{A}{2})-si{n}^{2}(π-\frac{A}{2})}$+cos2A=$\frac{[-cos2A-1]•(-sin\frac{A}{2})•cos\frac{A}{2}}{{cos}^{2}\frac{A}{2}{-sin}^{2}\frac{A}{2}}$+cos2A
=$\frac{-{2cos}^{2}A•(-\frac{1}{2})sinA}{cosA}$+cos2A=sinAcosA+cos2A=$\frac{1}{2}$sin2A+$\frac{1+cos2A}{2}$=$\frac{\sqrt{2}}{2}$sin(A+$\frac{π}{4}$)+$\frac{1}{2}$≤$\frac{\sqrt{2}+1}{2}$,
故f(A)的最大值为$\frac{\sqrt{2}+1}{2}$,
故选:A.
点评 本题主要考查三角恒等变换,正弦函数的值域,属于中档题.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
2.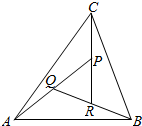 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )
 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )| A. | $\frac{2}{7},\frac{4}{7}$ | B. | $\frac{1}{2},\frac{1}{4}$ | C. | $\frac{1}{6},\frac{2}{7}$ | D. | $\frac{1}{6},\frac{3}{7}$ |
3.sin(-$\frac{9π}{2}$)的值为( )
| A. | 1 | B. | -1 | C. | 0 | D. | $\frac{\sqrt{2}}{2}$ |
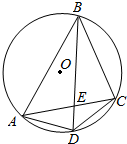 如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于点E.
如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于点E.