题目内容
18.已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积等于1 cm3.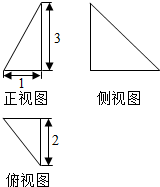
分析 根据几何体的三视图,得出该几何体是底面为直角三角形的直三棱锥,结合图中数据求出它的体积.
解答 解:根据几何体的三视图,得;
该几何体是底面为直角三角形,高为3的直三棱锥;
它的体积为V=$\frac{1}{3}$×$\frac{1}{2}$×1×2×3=1(cm3).
故答案为:1.
点评 本题考查了利用三视图求几何体体积的应用问题,是基础题目.

练习册系列答案
相关题目
6.等比数列{an}中,已知a1=3,an=96,其前n顶和Sn=189,则n的值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
13.已知角A为锐角,则f(A)=$\frac{[cos(π-2A)-1]sin(π+\frac{A}{2})sin(\frac{π}{2}-\frac{A}{2})}{si{n}^{2}(\frac{π}{2}-\frac{A}{2})-si{n}^{2}(π-\frac{A}{2})}$+cos2A的最大值为( )
| A. | $\frac{\sqrt{2}+1}{2}$ | B. | $\frac{\sqrt{2}-1}{2}$ | C. | $\frac{\sqrt{3}-1}{4}$ | D. | $\frac{\sqrt{3}+1}{4}$ |
3.若先将函数y=sin(4x+$\frac{π}{6}$)图象上各点的纵坐标不变,横坐标伸长到原来的2倍,再将所得图象向左平移$\frac{π}{6}$个单位,则所得函数图象的一条对称轴的方程是( )
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{2}$ |
8.先把函数y=cosx的图象上所有点向右平移$\frac{π}{3}$个单位,再把所得各点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),得到的函数图象的解析式为( )
| A. | y=cos(2x+$\frac{π}{3}$) | B. | y=cos(2x-$\frac{π}{3}$) | C. | y=cos($\frac{1}{2}$x+$\frac{π}{3}$) | D. | y=cos($\frac{1}{2}$x-$\frac{π}{3}$) |
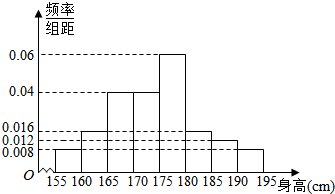 从某校高二年级800名学生中随机抽取100名测量身高,得到频率分布直方图如图.
从某校高二年级800名学生中随机抽取100名测量身高,得到频率分布直方图如图.