题目内容
20.直线l1,l2相交于点P,并且分别与平面γ相交于点A,B两点,用符号表示为l1∩l2=P,l1∩平面γ=A,l2∩平面γ=B.分析 利用直线与直线相交、直线与平面相交的符号、性质求解.
解答 解:∵直线l1,l2相交于点P,并且分别与平面γ相交于点A,B两点,
∴l1∩l2=P,l1∩平面γ=A,l2∩平面γ=B.
故答案为:l1∩l2=P,l1∩平面γ=A,l2∩平面γ=B.
点评 本题考查直线与直线相交、直线与平面相交的数学符号的应用,是基础题,解题时要认真审题,注意直线与直线相交、直线与平面相交的性质的合理运用.

练习册系列答案
相关题目
9.直线x-y-3=0与圆(x-1)2+y2=2的位置关系( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法判断 |
13.已知角A为锐角,则f(A)=$\frac{[cos(π-2A)-1]sin(π+\frac{A}{2})sin(\frac{π}{2}-\frac{A}{2})}{si{n}^{2}(\frac{π}{2}-\frac{A}{2})-si{n}^{2}(π-\frac{A}{2})}$+cos2A的最大值为( )
| A. | $\frac{\sqrt{2}+1}{2}$ | B. | $\frac{\sqrt{2}-1}{2}$ | C. | $\frac{\sqrt{3}-1}{4}$ | D. | $\frac{\sqrt{3}+1}{4}$ |
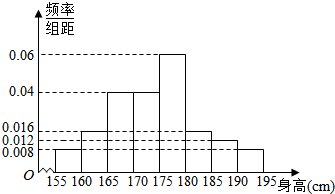 从某校高二年级800名学生中随机抽取100名测量身高,得到频率分布直方图如图.
从某校高二年级800名学生中随机抽取100名测量身高,得到频率分布直方图如图.