题目内容
已知球的直径SC=4,A,B是该球球面上的两点,∠ASC=∠BSC=30°,且AB=2,则三棱锥S-ABC的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:棱柱、棱锥、棱台的体积,球内接多面体
专题:空间位置关系与距离
分析:由已知得∠SAC=∠SBC=90°,∠SCA=∠SCB=60°,AC=BC=2,SA=SB=2
,取AB中点D,CD=
=
,S△ABC=
×2×
=
,SD=
=
,由余弦定理求出cos∠SCD=
,从而得到sin∠SCD=
,进而得到S到平面ABC的距离h=SC•sin∠SCD=
,由此能求出三棱锥S-ABC的体积.
| 3 |
| 4-1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 12-1 |
| 11 |
| ||
| 3 |
| ||
| 3 |
4
| ||
| 3 |
解答:
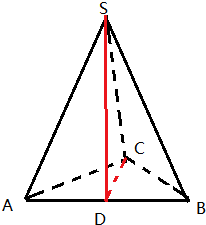 解:如图,∵球的直径SC=4,A,B是该球球面上的两点,
解:如图,∵球的直径SC=4,A,B是该球球面上的两点,
∠ASC=∠BSC=30°,且AB=2,
∴∠SAC=∠SBC=90°,∠SCA=∠SCB=60°,
∴AC=BC=2,SA=SB=2
,取AB中点D,CD=
=
,
S△ABC=
×2×
=
,
∵SA=SB,D为AB中点,∴SD⊥AB,
SD=
=
,
∴cos∠SCD=
=
=
,
sin∠SCD=
=
,
∴S到平面ABC的距离h=SC•sin∠SCD=
,
∴三棱锥S-ABC的体积V=
×
×
=
.
故选:D.
 解:如图,∵球的直径SC=4,A,B是该球球面上的两点,
解:如图,∵球的直径SC=4,A,B是该球球面上的两点,∠ASC=∠BSC=30°,且AB=2,
∴∠SAC=∠SBC=90°,∠SCA=∠SCB=60°,
∴AC=BC=2,SA=SB=2
| 3 |
| 4-1 |
| 3 |
S△ABC=
| 1 |
| 2 |
| 3 |
| 3 |
∵SA=SB,D为AB中点,∴SD⊥AB,
SD=
| 12-1 |
| 11 |
∴cos∠SCD=
| SC2+CD2-SD2 |
| 2SC•CD |
| 16+3-11 | ||
2×4×
|
| ||
| 3 |
sin∠SCD=
1-(
|
| ||
| 3 |
∴S到平面ABC的距离h=SC•sin∠SCD=
4
| ||
| 3 |
∴三棱锥S-ABC的体积V=
| 1 |
| 3 |
4
| ||
| 3 |
| 3 |
4
| ||
| 3 |
故选:D.
点评:本题考查三棱锥体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
等差数列{an}中,其前n项和为Sn,若a2+a5+a8=12,则S9为( )
| A、18 | B、72 |
| C、36 | D、无法确定 |
函数f(x)=log5(1-x)的定义域是( )
| A、(1,+∞) |
| B、(0,+∞) |
| C、(-∞,1) |
| D、(0,1] |
下列关系正确的是( )
| A、30.8>30.7 |
| B、1.72.5>1.73 |
| C、0.8-0.1>0.8-0.2 |
| D、1.012.7>1.013.5 |
设cosα=-
,α∈(0,π),则α的值可表示为( )
| 1 |
| 6 |
A、arccos
| ||
B、-arccos
| ||
C、π-arccos
| ||
D、π+arccos
|
若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
那么方程x3+x2-2x-2=0的一个近似根(精确度为0.05)为( )
| f(1)=-2 | f(1.5)=0.625 |
| f(1.25)=-0.984 | f(1.375)=-0.260 |
| f(1.438)=0.165 | f(1.4065)=-0.052 |
| A、1.275 | B、1.375 |
| C、1.415 | D、1.5 |
在实数运算中,定义新运算“⊕”如下:当a≥b时,a⊕b=a; 当a<b时,a⊕b=b2.则函数f(x)=(1⊕x)-(2⊕x)(其中x∈[-2,2])的最大值是( )(“-”仍为通常的减法)
| A、0 | B、2 | C、4 | D、6 |
在△ABC中,角A,B,C的对边分别为a,b,c,若cos(A-C)=1-cosB,a=2c,则cos2C的值为( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|