题目内容
若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
那么方程x3+x2-2x-2=0的一个近似根(精确度为0.05)为( )
| f(1)=-2 | f(1.5)=0.625 |
| f(1.25)=-0.984 | f(1.375)=-0.260 |
| f(1.438)=0.165 | f(1.4065)=-0.052 |
| A、1.275 | B、1.375 |
| C、1.415 | D、1.5 |
考点:二分法求方程的近似解
专题:函数的性质及应用
分析:按照二分法的方法流程进行计算,根据f(a)•f(b)的符号确定根所在的区间,当区间长度小于或等于0.05时,只需从该区间上任取一个数即可.
解答:
解:设近似根为x0,因为f′(x)=3x2+2x-2,其对称轴为x=-
,且f′(1)=3>0,f′(1.5)>0,所以原函数在区间(1,1.5)上是单调增函数;
因为f(1)f(1.5)<0,所以x0∈(1,1.5);
取x=
=1.25,∵f(1.25)=-0.984<0,f(1.5)=0.625>0,∴x0∈(1.25,1.5);
取x=
=1.375,∵f(1.375)=-0.260<0,又f(1.5)=0.625>0,∴{x0x0∈(1.375,1.5);
取x=
=1.438,∵f(1.438)=0.165>0,又f(1.375)=-0.260<0,∴x0∈(1.375,1.438),此时|1.438-1.375|=0.063>0.05;
再取x=
=1.4065,∵f(1.4065)=-0.052<0,又f(1.438)=0.165>0,∴x0∈(1.4065,1.438),此时|1.4065-1.438|=0.0315<0.05;
∵1.415∈(1.4065,1.438),∴取x0=1.415.
故选C.
| 1 |
| 3 |
因为f(1)f(1.5)<0,所以x0∈(1,1.5);
取x=
| 1+1.5 |
| 2 |
取x=
| 1.25+1.5 |
| 2 |
取x=
| 1.375+1.5 |
| 2 |
再取x=
| 1.375+1.438 |
| 2 |
∵1.415∈(1.4065,1.438),∴取x0=1.415.
故选C.
点评:本题考查了二分法求近似根的解法步骤,在解题时要注意先判断该解区间是否单调,然后再进行计算,此类题计算量较大,要避免计算错误.

练习册系列答案
相关题目
已知抛物线y2=4x,以(1,1)为中点作抛物线的弦,则这条弦所在直线的方程为( )
| A、x-2y+1=0 |
| B、2x-y-1=0 |
| C、2x+y-3=0 |
| D、x+2y-3=0 |
若一个圆的圆心在直线y=2x上,经过点(
,
),且与直线x-y+
=0相切,则这个圆的方程可能是( )
| ||
| 2 |
| ||
| 2 |
| 2 |
| A、x2+y2+x-2y=0 |
| B、x2+y2-2x+4y=0 |
| C、x2+y2-1=0 |
| D、x2+y2-2=0 |
斜边长为2的直角三角形的面积的最大值为( )
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
已知球的直径SC=4,A,B是该球球面上的两点,∠ASC=∠BSC=30°,且AB=2,则三棱锥S-ABC的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
集合A={x|x≥1},B={x|-1<x<2},则A∩B=( )
| A、{x|1<x<2} |
| B、{x|x>-1} |
| C、{x|1≤x<2} |
| D、{x|-1<x<2} |
设全集U=R,集合M={x|x>1},P={x|x2>1},则下列关系中正确的是( )
| A、M=P |
| B、P?M |
| C、∁U(M∩P)=∅ |
| D、M?P |
 如图,在△ABC中,M是AC的中点,点E在AB上,且AE=
如图,在△ABC中,M是AC的中点,点E在AB上,且AE=| 1 |
| 4 |
| A、2:1 | B、3:1 |
| C、3:2 | D、4:1 |
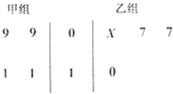 如图茎叶图记录了甲、乙两个组四名同学的植树棵树.乙组记录中有一个数计模糊,无法确认,在图中以X表示.
如图茎叶图记录了甲、乙两个组四名同学的植树棵树.乙组记录中有一个数计模糊,无法确认,在图中以X表示.