题目内容
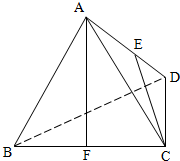如图，正四面体ABCD中，E为AD中点，F为BC中点，（1）求异面直线AB与CE所成角的大小；
（2）求异面直线AF与CE所成角的大小；
（3）求直线CE与平面BCD所成角的大小．
考点：直线与平面所成的角,异面直线及其所成的角
专题：空间角
分析：如图所示，建立空间直角坐标系．不妨设AB=6．则C（3，
，0），B（0，-2
，0），D（-3，
，0），A（0，0，2
），E(-
，
，
)，F(
，-
，0)．分别利用向量的夹角cos＜
，
＞=
，cos＜
，
＞=
即可得出异面直线所成的夹角．取平面BCD的法向量为
=（0，0，1）．
设直线CE与平面BCD所成角的大小为θ．利用sinθ=|cos＜
，
＞|=
即可得出线面角．
| 3 |
| 3 |
| 3 |
| 6 |
| 3 |
| 2 |
| ||
| 2 |
| 6 |
| 3 |
| 2 |
| ||
| 2 |
| AB |
| CE |
| ||||
|
|
| AF |
| CE |
| ||||
|
|
| n |
设直线CE与平面BCD所成角的大小为θ．利用sinθ=|cos＜
| n |
| CE |
|
| ||||
|
|
解答：
解：如图所示，建立空间直角坐标系．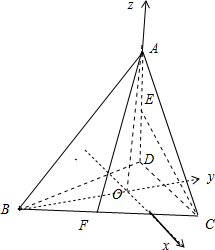
不妨设AB=6．则C（3，
，0），B（0，-2
，0），D（-3，
，0），A（0，0，2
），E(-
，
，
)，F(
，-
，0)．（1）∵
=(0，-2
，-2
)，
=(-
，-
，
)．
∴cos＜
，
＞=
=
=-
．
∴异面直线AB与CE所成角为arccos
；
（2）
=(
，-
，-2
)．
∴cos＜
，
＞=
=
=-
．
∴异面直线AF与CE所成角为arccos
．
（3）取平面BCD的法向量为
=（0，0，1）．
设直线CE与平面BCD所成角的大小为θ．
则sinθ=|cos＜
，
＞|=
=
=
．
∴直线CE与平面BCD所成角的大小为arcsin
．
不妨设AB=6．则C（3，
| 3 |
| 3 |
| 3 |
| 6 |
| 3 |
| 2 |
| ||
| 2 |
| 6 |
| 3 |
| 2 |
| ||
| 2 |
| AB |
| 3 |
| 6 |
| CE |
| 9 |
| 2 |
| ||
| 2 |
| 6 |
∴cos＜
| AB |
| CE |
| ||||
|
|
| -9 | ||
6×
|
| ||
| 6 |
∴异面直线AB与CE所成角为arccos
| ||
| 6 |
（2）
| AF |
| 3 |
| 2 |
| ||
| 2 |
| 6 |
∴cos＜
| AF |
| CE |
| ||||
|
|
| -18 | ||||
|
| 2 |
| 3 |
∴异面直线AF与CE所成角为arccos
| 2 |
| 3 |
（3）取平面BCD的法向量为
| n |
设直线CE与平面BCD所成角的大小为θ．
则sinθ=|cos＜
| n |
| CE |
|
| ||||
|
|
| ||
1×
|
| ||
| 3 |
∴直线CE与平面BCD所成角的大小为arcsin
| ||
| 3 |
点评：本题考查了通过建立空间直角坐标系利用向量的夹角公式求出异面直线所成的夹角、线面角，考查了推理能力和计算能力，考查了空间想象能力，属于难题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目