题目内容
已知函数f(x)=x2+ax+6.
(1)解不等式f(x)<0;
(2)若不等式f(x)>0对x<0恒成立,求a的范围.
(1)解不等式f(x)<0;
(2)若不等式f(x)>0对x<0恒成立,求a的范围.
考点:函数恒成立问题,二次函数的性质
专题:综合题,不等式的解法及应用
分析:(1)分△≤0,△>0两种情况进行讨论,结合二次函数的图象可得解集;
(2)分离出参数a后化为函数最值即可,利用基本不等式可求函数的最小值;
(2)分离出参数a后化为函数最值即可,利用基本不等式可求函数的最小值;
解答:
解:(1)f(x)<0即x2+ax+6<0,
△=a2-24,
当△≤0,即a≤-2
或a≥2
时,解集为∅;
当△>0即-2
<a<2
时,方程f(x)=0的根为x1,2=
,
f(x)<0的解集为:{x|
<a<
}.
综上,当a≤-2
或a≥2
时,不等式的解集为∅;当-2
<a<2
时,不等式的解集为{x|
<a<
}.
(2)f(x)>0即x2+ax+6>0恒成立,
当x<0时,可化为a<-x-
,
而-x-
≥2
=2
,当且仅当x=-
时取等号,
∴a<2
.
△=a2-24,
当△≤0,即a≤-2
| 6 |
| 6 |
当△>0即-2
| 6 |
| 6 |
-a±
| ||
| 2 |
f(x)<0的解集为:{x|
-a-
| ||
| 2 |
-a+
| ||
| 2 |
综上,当a≤-2
| 6 |
| 6 |
| 6 |
| 6 |
-a-
| ||
| 2 |
-a+
| ||
| 2 |
(2)f(x)>0即x2+ax+6>0恒成立,
当x<0时,可化为a<-x-
| 6 |
| x |
而-x-
| 6 |
| x |
(-x)•(
|
| 6 |
| 6 |
∴a<2
| 6 |
点评:该题考查函数恒成立、二次不等式的解法,考查分类讨论思想,深刻理解“三个二次”间的关系是解题关键.

练习册系列答案
相关题目
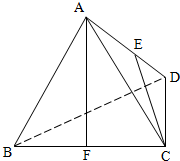 如图,正四面体ABCD中,E为AD中点,F为BC中点,
如图,正四面体ABCD中,E为AD中点,F为BC中点,