题目内容
函数y=x
+（1-x）
，0≤x≤1的最小值为 ．
| 3 |
| 2 |
| 3 |
| 2 |
考点：函数的最值及其几何意义
专题：转化思想,函数的性质及应用
分析：通过x+（1-x）=1，且0≤x≤1我们可以把函数转化为三角函数，在通过有最大最小值的函数，他的最值一定是在导数为0的地方来求解．
解答：
解：∵x+（1-x）=1，且0≤x≤1
∴可以令x=sin2α，1-x=cos2α
∴y=x
+（1-x）
=sin3α+cos3α
∴y′=3sin2αcosα-3cos2αsin2α
因为这个这个函数必定有最值，所以最值一定在导数为0的地方取得
∴可令y′=0
∴α={
，kπ+
}
代入求得最小值为：
y=-
∴可以令x=sin2α，1-x=cos2α
∴y=x
| 3 |
| 2 |
| 3 |
| 2 |
=sin3α+cos3α
∴y′=3sin2αcosα-3cos2αsin2α
因为这个这个函数必定有最值，所以最值一定在导数为0的地方取得
∴可令y′=0
∴α={
| kπ |
| 2 |
| π |
| 4 |
代入求得最小值为：
y=-
| ||
| 2 |
点评：通过观察可以发现x+（1-x）=1，故可以联想到三角函数，并转化为三角函数的最值问题．我们也可以得出只要两个数的和为1，都可以用三角函数进行代换．
练习册系列答案
名校课堂系列答案
相关题目
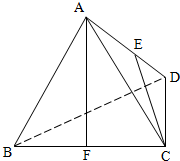如图，正四面体ABCD中，E为AD中点，F为BC中点，