题目内容
已知数列{an},an=
,求Sn.
| 1 |
| 2n(2n-1) |
考点:数列的求和
专题:等差数列与等比数列
分析:利用裂项求和法和泰勒级数求解.
解答:
解:∵an=
=
-
,
∴Sn=1-
+
-
+…+
-
把ln(x+1)按泰勒级数展开得:
ln(x+1)=x-
x2+
x3-
x4+…+
x2n-1-
x2n
取x=1,则1-
+
-
+
-
+…+
-
=ln2.
| 1 |
| 2n(2n-1) |
| 1 |
| 2n-1 |
| 1 |
| 2n |
∴Sn=1-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
把ln(x+1)按泰勒级数展开得:
ln(x+1)=x-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
取x=1,则1-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
若函数y=f(x)在(0,+∞)上的导函数为f′(x),且不等式xf′(x)>f(x)恒成立,又常数a,b满足a>b>0,则下列不等式一定成立的是( )
| A、af(a)>bf(b) |
| B、bf(a)<af(b) |
| C、bf(a)>af(b) |
| D、af(a)<bf(b) |
集合M={0},N={x∈Z|-1<x<1},则M∩N等于( )
| A、{-1,1} | B、{-1} |
| C、{1} | D、{0} |
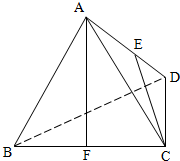 如图,正四面体ABCD中,E为AD中点,F为BC中点,
如图,正四面体ABCD中,E为AD中点,F为BC中点,