题目内容
求下列各函数的导数：
（1）y=3x2+xsinx
（2）y=
（3）y=xcos（2x）
（1）y=3x2+xsinx
（2）y=
| x2 |
| x+3 |
（3）y=xcos（2x）
考点：导数的乘法与除法法则
专题：函数的性质及应用
分析：利用导数的运算法则求解．
解答：
解：（1）∵y=3x2+xsinx，
∴y′=6x+sinx+xcosx．
（2）∵y=
，
∴y′=
=
．
（3）∵y=xcos（2x），
∴y′=cos（2x）-2xsin（2x）．
∴y′=6x+sinx+xcosx．
（2）∵y=
| x2 |
| x+3 |
∴y′=
| 2x(x+3)-x2 |
| (x+3)2 |
=
| x2+3 |
| (x+3)2 |
（3）∵y=xcos（2x），
∴y′=cos（2x）-2xsin（2x）．
点评：本题考查导数的求法，是基础题，解题时要注意导数的运算法则的合理运用．
练习册系列答案
相关题目
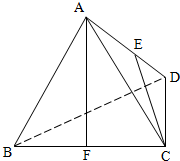如图，正四面体ABCD中，E为AD中点，F为BC中点，