题目内容
已知角α的终边过点P(-4,3).
(Ⅰ)求
的值;
(Ⅱ)若β为第三象限角,且tanβ=
,求cos(α-β)的值.
(Ⅰ)求
| tanα | ||
sin(π-α)-cos(
|
(Ⅱ)若β为第三象限角,且tanβ=
| 4 |
| 3 |
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:(Ⅰ)由条件利用任意角的三角函数的定义求出sinα 和cosα、tanα 的值,再根据
=
,计算求得结果.
(Ⅱ)由条件求得cosβ 和sinβ 的值,再根据cos(α-β)=cosαcosβ+sinαsinβ,计算求得结果.
| tanα | ||
sin(π-α)-cos(
|
| tanα |
| sinα+sinα |
(Ⅱ)由条件求得cosβ 和sinβ 的值,再根据cos(α-β)=cosαcosβ+sinαsinβ,计算求得结果.
解答:
解:(Ⅰ)∵角α的终边过点P(-4,3),故有 r=|OP|=5,sinα=
=
,cosα=
=-
,
∴tanα=
=-
,∴
=
=
=-
.
(Ⅱ)若β为第三象限角,且tanβ=
,则cosβ=-
,sinβ=-
,
∴cos(α-β)=cosαcosβ+sinαsinβ=-
×(-
)+
×(-
)=0.
| y |
| r |
| 3 |
| 5 |
| x |
| r |
| 4 |
| 5 |
∴tanα=
| y |
| x |
| 3 |
| 4 |
| tanα | ||
sin(π-α)-cos(
|
| tanα |
| sinα+sinα |
-
| ||
2×
|
| 5 |
| 8 |
(Ⅱ)若β为第三象限角,且tanβ=
| 4 |
| 3 |
| 3 |
| 5 |
| 4 |
| 5 |
∴cos(α-β)=cosαcosβ+sinαsinβ=-
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
点评:本题主要考查任意角的三角函数的定义,同角三角函数的基本关系,两角差的余弦公式,属于基础题.

练习册系列答案
相关题目
集合M={0},N={x∈Z|-1<x<1},则M∩N等于( )
| A、{-1,1} | B、{-1} |
| C、{1} | D、{0} |
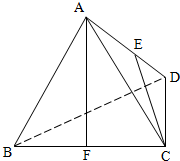 如图,正四面体ABCD中,E为AD中点,F为BC中点,
如图,正四面体ABCD中,E为AD中点,F为BC中点,