题目内容
设函数f(x)=(1+x)2-21n(1+x).
(1)求f(x)的单调区间;
(2)试讨论关于x的方程:f(x)=x2+x+a在区间[0,2]上的根的个数.
(1)求f(x)的单调区间;
(2)试讨论关于x的方程:f(x)=x2+x+a在区间[0,2]上的根的个数.
考点:利用导数研究函数的单调性,根的存在性及根的个数判断
专题:导数的综合应用
分析:(1)求函数的导数,即可求f(x)的单调区间;
(2)利用参数分离法,转化为a=1+x-21n(1+x),然后利用导数求出g(x)=1+x-21n(1+x)在区间[0,2]上的极值和最值即可得到结论.
(2)利用参数分离法,转化为a=1+x-21n(1+x),然后利用导数求出g(x)=1+x-21n(1+x)在区间[0,2]上的极值和最值即可得到结论.
解答:
解:(1)函数的定义域为(-1,+∞),
则函数的导数f′(x)=2(x+1)-
=
,
若f′(x)>0,则x>0,此时函数单调递增,
若f′(x)<0,则-1<x<0,此时函数单调递减,
即f(x)的单调增区间为(0,+∞);
f(x)的单调减区间为(-1,0);
(2)由f(x)=x2+x+a,
得(1+x)2-21n(1+x)=x2+x+a,
则a=1+x-21n(1+x),
设g(x)=1+x-21n(1+x),
则g′(x)=1-
=
,
当1<x<2时,g′(x)>0,此时函数g(x)单调递增,
当0<x<1时,g′(x)<0,此时函数g(x)单调递减,
即当x=1时,函数g(x)取得极小值,同时也是最小值g(1)=2-2ln2,
∵g(0)=1,g(2)=3-2ln3<1,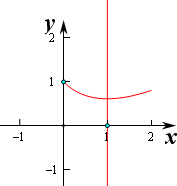
∴若a<2-2ln2,则方程a=1+x-21n(1+x)在区间[0,2]无解,
若a=2-2ln2,则方程a=1+x-21n(1+x)在区间[0,2]有1解,
若2-2ln2<a≤3-2ln3,则方程a=1+x-21n(1+x)在区间[0,2]有2解,
若3-2ln3<a≤1,则方程a=1+x-21n(1+x)在区间[0,2]有1解,
若a>1则方程a=1+x-21n(1+x)在区间[0,2]无解.
则函数的导数f′(x)=2(x+1)-
| 2 |
| 1+x |
| 2x(x+2) |
| x+1 |
若f′(x)>0,则x>0,此时函数单调递增,
若f′(x)<0,则-1<x<0,此时函数单调递减,
即f(x)的单调增区间为(0,+∞);
f(x)的单调减区间为(-1,0);
(2)由f(x)=x2+x+a,
得(1+x)2-21n(1+x)=x2+x+a,
则a=1+x-21n(1+x),
设g(x)=1+x-21n(1+x),
则g′(x)=1-
| 2 |
| 1+x |
| x-1 |
| x+1 |
当1<x<2时,g′(x)>0,此时函数g(x)单调递增,
当0<x<1时,g′(x)<0,此时函数g(x)单调递减,
即当x=1时,函数g(x)取得极小值,同时也是最小值g(1)=2-2ln2,
∵g(0)=1,g(2)=3-2ln3<1,

∴若a<2-2ln2,则方程a=1+x-21n(1+x)在区间[0,2]无解,
若a=2-2ln2,则方程a=1+x-21n(1+x)在区间[0,2]有1解,
若2-2ln2<a≤3-2ln3,则方程a=1+x-21n(1+x)在区间[0,2]有2解,
若3-2ln3<a≤1,则方程a=1+x-21n(1+x)在区间[0,2]有1解,
若a>1则方程a=1+x-21n(1+x)在区间[0,2]无解.
点评:本题主要考查函数的单调性和导数的关系,以及方程根的个数的判断,考查学生的推理能力.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
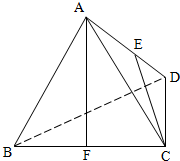 如图,正四面体ABCD中,E为AD中点,F为BC中点,
如图,正四面体ABCD中,E为AD中点,F为BC中点,