题目内容
已知X的分布列为P(X=k)=
(k=1,2,…,6),其中c为常数,则P(X≤2)= .
| c |
| 2k |
考点:离散型随机变量及其分布列
专题:概率与统计
分析:利用X的分布列先求出c的值,再计算P(X≤2)=P(X=1)+P(X=2)的值.
解答:
解:∵X的分布列为P(X=k)=
(k=1,2,…,6),其中c为常数,
∴
+
+
+
+
+
=1,
解得c=
P(X≤2)=P(X=1)+P(X=2)
=
+
=
c=
×
=
.
故答案为:
.
| c |
| 2k |
∴
| c |
| 2 |
| c |
| 22 |
| c |
| 23 |
| c |
| 24 |
| c |
| 25 |
| c |
| 26 |
解得c=
| 32 |
| 63 |
P(X≤2)=P(X=1)+P(X=2)
=
| c |
| 2 |
| c |
| 22 |
| 3 |
| 4 |
| 3 |
| 4 |
| 32 |
| 63 |
| 8 |
| 21 |
故答案为:
| 8 |
| 21 |
点评:本题考查概率的求法,是基础题,解题时要认真审题,注意离散型随机变量的分布列的性质的灵活运用.

练习册系列答案
相关题目
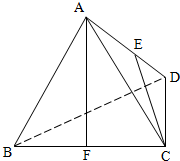 如图,正四面体ABCD中,E为AD中点,F为BC中点,
如图,正四面体ABCD中,E为AD中点,F为BC中点,