题目内容
设
=(1,2),
=(2,k),若(2
+
)⊥
,则实数k的值为( )
| a |
| b |
| a |
| b |
| a |
| A、-2 | B、-4 | C、-6 | D、-8 |
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:求出向量2
+
,然后利用向量的数量积为0求解即可.
| a |
| b |
解答:
解:
=(1,2),
=(2,k),
∴2
+
=(4,4+k),
∵(2
+
)⊥
,
∴(2
+
)•
=0,
即4+8+2k=0,
解得k=-6.
故选:C.
| a |
| b |
∴2
| a |
| b |
∵(2
| a |
| b |
| a |
∴(2
| a |
| b |
| a |
即4+8+2k=0,
解得k=-6.
故选:C.
点评:本题考查向量的基本运算,向量的垂直体积的应用,基本知识的考查.

练习册系列答案
相关题目
若y=f(2x)的图象关于直线x=
和x=
(b>a)对称,则f(x)的一个周期为( )
| a |
| 2 |
| b |
| 2 |
A、
| ||
| B、2(b-a) | ||
C、
| ||
| D、4(b-a) |
已知数列{an}是等比数列,Sn是其前n项和,且a3=2,S3=6,则a5=( )
A、2或-
| ||
B、
| ||
| C、±2 | ||
D、2或
|
若m>0,n>0,a>0且a≠1,则下列等式中正确的是( )
| A、(am)n=am+n | |||||
B、a
| |||||
| C、logam÷logan=loga(m-n) | |||||
D、
|
如图给出的是计算
+
+
+…+
的值的程序框图,其中判断框内应填入的是( )
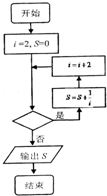
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2014 |

| A、i≤2013 |
| B、i≤2015 |
| C、i≤2017 |
| D、i≤2019 |
已知sin(π+α)=
,且α是第四象限角,则cos(α-2π)的值是( )
| 2 |
| 3 |
A、±
| ||||
B、
| ||||
C、±
| ||||
D、
|
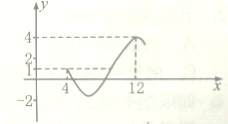 如图为函数f(x)=Asin(ωx+φ)+C(A>0,ω>0,0<φ<π)图象的一部分.
如图为函数f(x)=Asin(ωx+φ)+C(A>0,ω>0,0<φ<π)图象的一部分.