Question

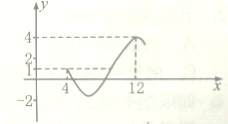如图为函数f（x）=Asin（ωx+φ）+C（A＞0，ω＞0，0＜φ＜π）图象的一部分．
（1）求函数f（x）的周期及单调区间．
（2）说明函数f（x）的图象可以由y=sinx（x∈R）得图象经过怎样的变换得到．
（3）求与函数f（x）图象关于直线x=2对称的函数y=g（x）的解析式．

Answer 1

考点：函数y=Asin（ωx+φ）的图象变换,正弦函数的图象

专题：三角函数的图像与性质

分析：（1）首先，确定振幅A和平衡位置，然后，根据周期公式求解ω的值，然后将点（4，1）代人确定φ的值；
（2）直接结合三角函数的平移变换公式进行求解；
（3）根据对称性直接求解其解析式．

解答： 解：（1）结合图象得
A=3，C=1，

3

4

T=12-4=8，
∴ω=

3π

16

，
∴y=3sin（

3π

16

x+∅）+1，
将点（4，1）代人，得
3sin（

3π

4

+∅）+1=1，
∴

3π

4

+φ=kπ，k∈Z，
∵0＜φ＜π，
∴φ=

π

4

，
∴y=3sin（

3π

16

x+

π

4

）+1，
∴周期为：T=

32

3

，
令-

π

2

+2kπ≤

3π

16

x+

π

4

≤

π

2

+2kπ，k∈Z，
得-4+

32

3

k≤x≤

4

3

+

32k

3

，
∴增区间为：[-4+

32

3

k，

4

3

+

32k

3

]，
令

π

2

+2kπ≤

3π

16

x+

π

4

≤

3π

2

+2kπ，k∈Z，
得

4

3

+

32

3

k≤x≤

20

3

+

32k

3

，
∴减区间为：[

3

4

+

32

3

k，

20

3

+

32k

3

]，
（2）首先，由y=sinx（x∈R）的图象上各点向左平移

π

4

个单位，
得到函数y=sin（x+

π

4

）的图象，然后，将所得函数图象上各点的横坐标缩短到原来的

16

3π

倍，得到
函数y=sin（

3π

16

x+

π

4

）的图象，然后，再将所得函数图象上各点的纵坐标伸长到原来的3倍，得到
函数y=3sin（

3π

16

x+

π

4

）的图象，然后，再将所得图象向上平移1个单位，即得函数y=3sin（

3π

16

x+

π

4

）+1的图象．
（3）设点P（x，y）是函数y=g（x）图象上任一点，
点P关于直线x=2的对称点为（x₀，y₀），
则y₀=3sin（

3π

16

x₀+

π

4

）+1，①
∵

x+x0 2 =2 y=y0

，
∴

x0=4-x y0=y

，将此代人①，得
y=3sin[

3π

16

（4-x）+

π

4

]+1
=3sin（π-x）+1
=1+3sinx，
∴函数y=g（x）的解析式g（x）=1+3sinx．

点评：本题重点考查了三角函数的图象与性质、三角函数诱导公式等知识，属于中档题．解题的关键是灵活运用对称思想求解函数的解析式．