题目内容

已知A，B，P是双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）上不同的三个点，且A，B的连线经过坐标原点，若直线PA、PB的斜率的乘积kPA•kPB=
1
3
，则该双曲线的离心率为
 
．
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设出点的坐标，求出斜率，将点的坐标代入方程，两式相减，再结合kPA•kPB=
1
3
，即可求得结论．
解答： 解：由题意，设A（x1，y1），P（x2，y2），则B（-x1，-y1）
∴kPA•kPB=
y22-y12
x22-x12
，
∵
x12
a2
-
y12
b2
=1，
x22
a2
-
y22
b2
=1
∴两式相减可得
y22-y12
x22-x12
=
b2
a2
，
∵kPA•kPB=
1
3
，
∴
b2
a2
=
1
3
，
∴e2=1+
b2
a2
=
4
3
，
∴e=
2
3
3
．
故答案为：
2
3
3
．
点评：本题考查双曲线的标准方程，以及双曲线的简单性质的应用，得到
b2
a2
=
1
3
是解题的关键．
练习册系列答案
相关题目
已知非零数列{an}的递推公式为a1=1，an=an•an+1+2an+1（n∈N*）
（1）求证：数列{1+
1
an
}是等比数列；
（2）若关于n的不等式
1
n+log2(1+
1
a1
)
+
1
n+log2(1+
1
a2
)
+…+
1
n+log2(1+
1
an
)
＜m-
5
2
有解，求整数m的最小值．
（3）在数列{
1
an
+1-（-1）n}（1≤n≤11）中，是否一定存在首项、第r项、第s项（1＜r＜s≤11），使得这三项依次成等差数列？若存在，请指出r、s所满足的条件；若不存在，请说明理由．
设正项数列{an}的前n项和为Sn，且
an
2
，
Sn
2
，
an+1
2
数列n（∈N*）
（1）求数列{an}的通项公式；
（2）设bn=
an
2n
数列{bn}中是否存在正整数对（m，n），当m＜n时使得{bn}中的三项b1，bm，bn ，成等差数列．若存在，求出m，n；若不存在，说明理由．
设函数f（x）=
x
 x≥0
-x
  x＜0
，若f（a）+f（-1）=3，则实数a=
 
．
若某程序框图如图所示，则该程序运行后输出的值等于
 
．
设函数f（x）的定义域为D，如果存在正实数k，使对任意x∈D，都有x+k∈D，且f（x+k）＞f（x）恒成立，则称函数f（x）为D上的“k型增函数”．已知f（x）是定义在R上的奇函数，且当x＞0时，f（x）=|x-a|-2a，若f（x）为R上的“2014型增函数”，则实数a的取值范围是
 
．
已知△ABC的周长为
2
+1，且sinA+sinB=
2
sinC．若△ABC的面积为
1
6
sinC，则角C的大小为（　　）
A、30°B、60°
C、90°D、120°
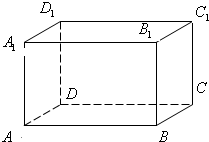如图，长方体ABCD-A1B1C1D1中，交于顶点A的三条棱长分别为AD=3，AA1=4，AB=5，则从A点沿表面到C1的最短距离为（　　）
A、5
2
B、
74
C、4
5
D、3
10
已知函数fn（x）=
x2-2x-a
enx
，其中n∈N*，a∈R，e是自然对数的底数．
（1）求函数g（x）=f1（x）-f2（x）的零点；
（2）若对任意n∈N*，fn（x）均有两个极值点，一个在区间（1，4）内，另一个在区间[1，4]外，求a的取值范围；
（3）已知k，m∈N*，k＜m，且函数fk（x）在R上是单调函数，探究函数fm（x）的单调性．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网