题目内容
设函数f(x)的定义域为D,如果存在正实数k,使对任意x∈D,都有x+k∈D,且f(x+k)>f(x)恒成立,则称函数f(x)为D上的“k型增函数”.已知f(x)是定义在R上的奇函数,且当x>0时,f(x)=|x-a|-2a,若f(x)为R上的“2014型增函数”,则实数a的取值范围是 .
考点:函数奇偶性的性质
专题:新定义,函数的性质及应用
分析:由题意结合奇函数的性质可得f(x)的解析式,再利用新定义对x分类讨论,结合绝对值的意义综合可得.
解答:
解:∵f(x)是定义在R上的奇函数,且当x>0时,f(x)=|x-a|-2a,
设x<0,则-x>0.∴f(-x)=|-x-a|-2a=|x+a|-2a,
∴f(x)=-f(-x)=-|x+a|+2a.
又由奇函数的性质可得f(0)=0.
∴f(x)=
,
又∵f(x)为R上的“2014型增函数”,
∴当x>0时,|x+2014-a|-2a>|x-a|-2a,即|x+2014-a|>|x-a|恒成立,
式子|x+2014-a|>|x-a|的几何意义为数轴上到点a的距离小于到点a-2014的距离,
又x>0,∴a+a-2014<0,解得a<1007;
当x<0<x+2014时,|x+2014-a|-2a>-|x+a|+2a,即|x+2014-a|+|x+a|>4a恒成立,
∴根据几何意义得|2a-2014|>4a,即a<
;
当x<x+2014<0时,-|x+2014+a|+2a>-|x+a|+2a,即|x+2014+a|<|x+a|恒成立,
∴-a-a-2014>0,即a<1007.
综上知:实数a的取值范围为a<
故答案为:a<
设x<0,则-x>0.∴f(-x)=|-x-a|-2a=|x+a|-2a,
∴f(x)=-f(-x)=-|x+a|+2a.
又由奇函数的性质可得f(0)=0.
∴f(x)=
|
又∵f(x)为R上的“2014型增函数”,
∴当x>0时,|x+2014-a|-2a>|x-a|-2a,即|x+2014-a|>|x-a|恒成立,
式子|x+2014-a|>|x-a|的几何意义为数轴上到点a的距离小于到点a-2014的距离,
又x>0,∴a+a-2014<0,解得a<1007;
当x<0<x+2014时,|x+2014-a|-2a>-|x+a|+2a,即|x+2014-a|+|x+a|>4a恒成立,
∴根据几何意义得|2a-2014|>4a,即a<
| 1007 |
| 3 |
当x<x+2014<0时,-|x+2014+a|+2a>-|x+a|+2a,即|x+2014+a|<|x+a|恒成立,
∴-a-a-2014>0,即a<1007.
综上知:实数a的取值范围为a<
| 1007 |
| 3 |
故答案为:a<
| 1007 |
| 3 |
点评:本题考查奇函数的性质、新定义、分类讨论和绝对值的意义等基础知识与基本技能方法,属中档题.

练习册系列答案
相关题目
某算法的程序框图如图所示,若输入a=1,b=2,c=3,则输出的结果为( )


| A、1 | B、2 | C、3 | D、4 |
(理)已知数列{an}的通项公式an=n2-(6+2λ)n+2014,若a6或a7为数列{an}的最小项,则实数λ的取值范围( )
| A、(3,4) | ||||
| B、[2,5] | ||||
| C、[3,4] | ||||
D、[
|
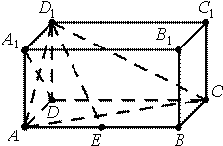 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.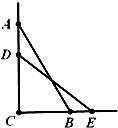 如图,一根长为2米的木棒AB斜靠在墙壁AC上,∠ABC=60°,若AB滑动至DE位置,
如图,一根长为2米的木棒AB斜靠在墙壁AC上,∠ABC=60°,若AB滑动至DE位置,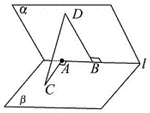 如图,60°的二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则CD的长为
如图,60°的二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则CD的长为