题目内容
已知函数fn(x)=
,其中n∈N*,a∈R,e是自然对数的底数.
(1)求函数g(x)=f1(x)-f2(x)的零点;
(2)若对任意n∈N*,fn(x)均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
(3)已知k,m∈N*,k<m,且函数fk(x)在R上是单调函数,探究函数fm(x)的单调性.
| x2-2x-a |
| enx |
(1)求函数g(x)=f1(x)-f2(x)的零点;
(2)若对任意n∈N*,fn(x)均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
(3)已知k,m∈N*,k<m,且函数fk(x)在R上是单调函数,探究函数fm(x)的单调性.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)表示出g(x)=f1(x)-f2(x)=
,ex-1有一零点0,只需讨论x2-2x-a的零点情况,△=4+4a,分△<0,△=0,△>0三种情况进行讨论可得‘
(2)fn′(x)=
=
,令gn(x)=-nx2+2(n+1)x+an-2,则问题等价于对任意n∈N*,gn(x)=0有两个不等实数根x1,x2,且x1∈(1,4),x2∉[1,4],进而由零点判定定理得对任意n∈N*,gn(1)gn(4)<0,化为恒成立可求;
(3)可知函数fk(x)在R上是单调减函数,从而f′k(x)<0,则△k=4(k+1)2+4k(ka-2)=4(k2a+k2+1)≤0,由此推导f′m(x)的符号可得结论;
| (x2-2x-a)(ex-1) |
| e2x |
(2)fn′(x)=
| (2x-2)enx-n(x2-2x-a)enx |
| e2nx |
| -nx2+2(n+1)x+an-2 |
| enx |
(3)可知函数fk(x)在R上是单调减函数,从而f′k(x)<0,则△k=4(k+1)2+4k(ka-2)=4(k2a+k2+1)≤0,由此推导f′m(x)的符号可得结论;
解答:
解:(1)g(x)=f1(x)-f2(x)=
-
=
,
△=4+4a,
①当a<-1时,△<0,函数g(x)有1个零点:x1=0;
②当a=-1时,△=0,函数g(x)有2个零点:x1=0,x2=1,;
③当a=0时,△>0,函数g(x)有两个零点:x1=0,x2=2;
④当a>-1,a≠0时,△>0函数g(x)有三个零点:x1=0,x2=1-
,x3=1+
;
(2)fn′(x)=
=
,
设gn(x)=-nx2+2(n+1)x+an-2,gn(x)的图象是开口向下的抛物线.
由题意对任意n∈N*,gn(x)=0有两个不等实数根x1,x2,且x1∈(1,4),x2∉[1,4],
则对任意n∈N*,gn(1)gn(4)<0,即n(a+1)•n•[a-(8-
)]<0,
又任意n∈N*,8-
关于n递增,8-
>-1,
故-1<a<(8-
)min,-1<a<8-6=2,
∴a的取值范围是(-1,2).
(3)由(2)知,存在x∈R,fk′(x)=
<0,
又函数fk(x)在R上是单调函数,故函数fk(x)在R上是单调减函数,
从而△k=4(k+1)2+4k(ka-2)=4(k2a+k2+1)≤0,即a≤-(1+
),
∴△m=4(m2+1+m2a)≤4[m2+1-m2(1+
)]=
,
由k,m∈N*,k<m,知△m<0,即对任意x∈R,f′m(x)=
<0,
故函数fm(x)在R上是减函数.
| x2-2x-a |
| ex |
| x2-2x-a |
| e2x |
| (x2-2x-a)(ex-1) |
| e2x |
△=4+4a,
①当a<-1时,△<0,函数g(x)有1个零点:x1=0;
②当a=-1时,△=0,函数g(x)有2个零点:x1=0,x2=1,;
③当a=0时,△>0,函数g(x)有两个零点:x1=0,x2=2;
④当a>-1,a≠0时,△>0函数g(x)有三个零点:x1=0,x2=1-
| a+1 |
| a+1 |
(2)fn′(x)=
| (2x-2)enx-n(x2-2x-a)enx |
| e2nx |
| -nx2+2(n+1)x+an-2 |
| enx |
设gn(x)=-nx2+2(n+1)x+an-2,gn(x)的图象是开口向下的抛物线.
由题意对任意n∈N*,gn(x)=0有两个不等实数根x1,x2,且x1∈(1,4),x2∉[1,4],
则对任意n∈N*,gn(1)gn(4)<0,即n(a+1)•n•[a-(8-
| 6 |
| n |
又任意n∈N*,8-
| 6 |
| n |
| 6 |
| n |
故-1<a<(8-
| 6 |
| n |
∴a的取值范围是(-1,2).
(3)由(2)知,存在x∈R,fk′(x)=
| -kx2+2(k+1)x+ak-2 |
| ekx |
又函数fk(x)在R上是单调函数,故函数fk(x)在R上是单调减函数,
从而△k=4(k+1)2+4k(ka-2)=4(k2a+k2+1)≤0,即a≤-(1+
| 1 |
| k2 |
∴△m=4(m2+1+m2a)≤4[m2+1-m2(1+
| 1 |
| k2 |
| 4(k2-m2) |
| k2 |
由k,m∈N*,k<m,知△m<0,即对任意x∈R,f′m(x)=
| -mx2+2(m+1)x+am-2 |
| emx |
故函数fm(x)在R上是减函数.
点评:本题考查利用导数研究函数的零点、极值点、单调性等知识,考查学生综合运用知识分析解决问题的能力,本题综合性较强,能力要求较高.

练习册系列答案
相关题目
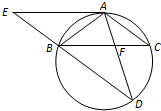 如图,△ABC为圆的内接三角形,AB=AC,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.
如图,△ABC为圆的内接三角形,AB=AC,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.