题目内容
已知非零数列{an}的递推公式为a1=1,an=an•an+1+2an+1(n∈N*)
(1)求证:数列{1+
}是等比数列;
(2)若关于n的不等式
+
+…+
<m-
有解,求整数m的最小值.
(3)在数列{
+1-(-1)n}(1≤n≤11)中,是否一定存在首项、第r项、第s项(1<r<s≤11),使得这三项依次成等差数列?若存在,请指出r、s所满足的条件;若不存在,请说明理由.
(1)求证:数列{1+
| 1 |
| an |
(2)若关于n的不等式
| 1 | ||
n+log2(1+
|
| 1 | ||
n+log2(1+
|
| 1 | ||
n+log2(1+
|
| 5 |
| 2 |
(3)在数列{
| 1 |
| an |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由已知条件推导了
-
=1,从而得到
+1=2(
+1),由此能证明{1+
}是等比数列.
(2)由(1)知1+
=2n,由题设条件得到
+
+…+
<m-
,令f(n)=
+
+…+
,由f(n)是增函数,能求出整数m的最小值.
(3)由已知条件推导出
+1+(-1)n=2n+(-1)n=bn,要使b1,br,bs成等差数列,只需b1+bs=2br,由此求出存在首项、第r项、第s项(1<r<s≤11),使得这三项依次成等差数列.
| 1 |
| an+1 |
| 2 |
| an |
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| an |
(2)由(1)知1+
| 1 |
| an |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+n |
| 5 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+n |
(3)由已知条件推导出
| 1 |
| an |
解答:
(1)证明:∵非零数列{an}的递推公式为a1=1,an=an•an+1+2an+1(n∈N*),
∴
-
=1,
∴
+1=2(
+1),
∴{1+
}是首项为2,公比为2的等比数列.
(2)解:∵{1+
}是首项为2,公比为2的等比数列,
∴1+
=2n,
∵
+
+…+
<m-
,
∴
+
+…+
=
+
+…+
<m-
,
令f(n)=
+
+…+
,
则f(n+1)-f(n)=
+
-
=
-
>0,
∴f(n)是增函数,
∴f(n)min=f(1)=
,
∴
<m-
.解得m>3,
∴整数m的最小值为4.
(3)∵1+
=2n,
∴an=
,
∴
+1+(-1)n=2n+(-1)n=bn,
要使b1,br,bs成等差数列,只需b1+bs=2br,
即2s-2r+1=(-1)s-2(-1)r-3,
∵s≥r+1,∴2s-2r+1≥0,
∵(-1)s-2(-1)r-3≤0,
∴当且仅当s=r+1,且s为不小于的偶数时,
存在首项、第r项、第s项(1<r<s≤11),使得这三项依次成等差数列.
∴
| 1 |
| an+1 |
| 2 |
| an |
∴
| 1 |
| an+1 |
| 1 |
| an |
∴{1+
| 1 |
| an |
(2)解:∵{1+
| 1 |
| an |
∴1+
| 1 |
| an |
∵
| 1 | ||
n+log2(1+
|
| 1 | ||
n+log2(1+
|
| 1 | ||
n+log2(1+
|
| 5 |
| 2 |
∴
| 1 | ||
n+log2(1+
|
| 1 | ||
n+log2(1+
|
| 1 | ||
n+log2(1+
|
=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+n |
| 5 |
| 2 |
令f(n)=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+n |
则f(n+1)-f(n)=
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
∴f(n)是增函数,
∴f(n)min=f(1)=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 5 |
| 2 |
∴整数m的最小值为4.
(3)∵1+
| 1 |
| an |
∴an=
| 1 |
| 2n-1 |
∴
| 1 |
| an |
要使b1,br,bs成等差数列,只需b1+bs=2br,
即2s-2r+1=(-1)s-2(-1)r-3,
∵s≥r+1,∴2s-2r+1≥0,
∵(-1)s-2(-1)r-3≤0,
∴当且仅当s=r+1,且s为不小于的偶数时,
存在首项、第r项、第s项(1<r<s≤11),使得这三项依次成等差数列.
点评:本题考查等比数列的证明,考查最小值的求法,考查数列中存在首项、第r项、第s项(1<r<s≤11),使得这三项依次成等差数列的证明,解题时要注意等价转化思想的合理运用.

练习册系列答案
相关题目
“a,b为异面直线”是指:
①a∩b=ϕ,且a与b不平行;
②a?平面α,b?平面β,且a∩b=ϕ;
③a?平面α,b?平面β,且α∩β=ϕ;
④a?平面α,b?平面α;
⑤不存在平面α,能使a?α且b?α成立.
上述结论中,正确的是( )
①a∩b=ϕ,且a与b不平行;
②a?平面α,b?平面β,且a∩b=ϕ;
③a?平面α,b?平面β,且α∩β=ϕ;
④a?平面α,b?平面α;
⑤不存在平面α,能使a?α且b?α成立.
上述结论中,正确的是( )
| A、①④⑤正确 | B、①⑤正确 |
| C、②④正确 | D、①③④正确 |
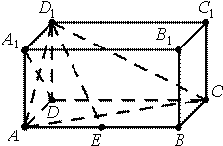 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.