题目内容
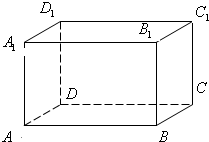如图，长方体ABCD-A1B1C1D1中，交于顶点A的三条棱长分别为AD=3，AA1=4，AB=5，则从A点沿表面到C1的最短距离为（ ）A、5
| ||
B、
| ||
C、4
| ||
D、3
|
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：从A点沿不同的表面到C1，其距离可采用将长方体展开的方式求得．
解答：
解：从A点沿不同的表面到C1，
其距离可采用将长方体展开的方式求得，
分别是
=
，
=4
，
=3
，
∴从A点沿表面到C1的最短距离为
．
故选：B．
其距离可采用将长方体展开的方式求得，
分别是
| (3+4)2+52 |
| 74 |
| (3+5)2+42 |
| 5 |
| (4+5)2+32 |
| 10 |
| 10 |
∴从A点沿表面到C1的最短距离为
| 74 |
故选：B．
点评：本题考查从A点沿表面到C1的最短距离的求法，是中档题，解题时要认真审题，注意分类讨论思想的合理运用．
练习册系列答案
相关题目
（理）已知数列{an}的通项公式an=n2-（6+2λ）n+2014，若a6或a7为数列{an}的最小项，则实数λ的取值范围（ ）
| A、（3，4） | ||||
| B、[2，5] | ||||
| C、[3，4] | ||||
D、[
|
若复数z=（a2+2a-3）+（a-l）i为纯虚数（i为虚数单位），则实数a的值为（ ）
| A、-3 | B、-3或1 |
| C、3或-1 | D、1 |
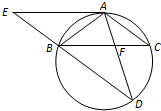如图，△ABC为圆的内接三角形，AB=AC，BD为圆的弦，且BD∥AC．过点A作圆的切线与DB的延长线交于点E，AD与BC交于点F．